Алгебра, вопрос задал fctdgsygfdhngfxzgsac , 11 месяцев назад

Розкласти многочлен на множники (виконати ділення многочлена кутом).

Приложения:

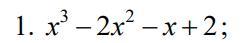
Ответы на вопрос

Ответил NNNLLL54

Ответ:

Здесь можно разложить на множители применив метод группировки .

$\bf x^3-2x^2-x+2=(x^3-2x^2)+(-x+2)=x^2\, (x-2)-(x-2)=\\\\=(x-2)(x^2-1)=(x-2)(x-1)(x+1)$

Если вам надо разделить многочлен , например, на (х-1) , то это так:

$\bf {}\ \ \ \ \ x^3-2x^2-x+2\ \ \ |\ x-1\\{}-(x^3-x^2)\qquad \qquad \ \ --------\\-------\qquad \qquad x^2-x-2\\{}\ \ -x^2-x+2\\{}\ -(-x^2+x)\\{}\ \ -------\\{}\ \ \qquad -2x+2\\{}\quad \quad -(-2x+2)\\{}\qquad ------- \\{}\qquad \qquad \qquad 0\\\\\\x^3-2x^2-x+2=(x-1)(x^2-x-2)=(x-1)(x-2)(x+1)$

Затем по теореме Виета найти корни квадратного трёхчлена , они будут равны х = -1 и х = 2 . Тогда получим то же разложение , что и методом группировки .

Приложения:

fctdgsygfdhngfxzgsac: спасибо большое)

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Қазақ тiлi, 11 месяцев назад

жоңғария очерктері оқырмандық ой пайым...

Алгебра, 11 месяцев назад

Скільки коренів має рівняння ||x| - 1| =а, в залежності від значення параметра а...

Геометрия, 11 месяцев назад

напишіть шось я бали віддам...

Биология, 11 месяцев назад

Визначте послідовність нуклеотидів у ділянці молекули і-РНК, синтезованої з ділянки ДНК такої структури: -Г – Ц – Т – А – А – Ц – Ц – Г – А – А – Г – Г – А -...

Английский язык, 6 лет назад

Please help choose the ccorect item.

Физика, 6 лет назад

помогите пжжжжж, нужен не только ответ, но и решение ...