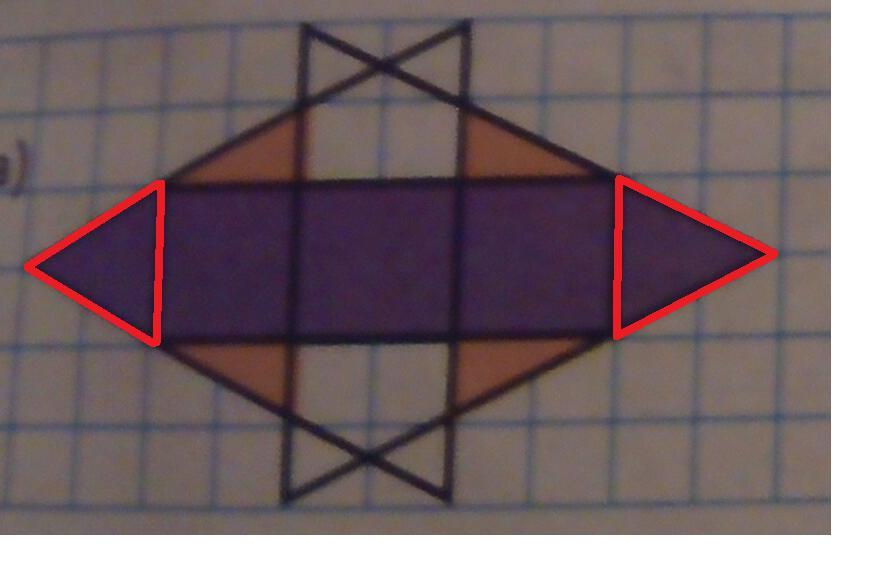
Рисунок к задаче. Найдите на рисунках все четные и нечетные вершины. Какой из рисунков можно сделать одним движением руки, не повторяя ни одной линии дважды? Один из рисунков раскрасили. Найдите площадь каждого цвета. Задача за 4 класс.

Ответы на вопрос
Ответ:
Четные вершины - это точки, в которых пересекается четное количество отрезков. На рисунке они помечены красным цветом.
Нечетные вершины - это точки, в которых пересекается нечетное количество отрезков. На рисунке они помечены желтым цветом.
Оказывается, чтобы узнать, какой рисунок можно сделать одним движением руки, не повторяя ни одной линии дважды, не обязательно пробовать его рисовать, а достаточно сосчитать нечетные вершины.
Есть такое правило:
- если нечетных вершин нет, то есть все вершины четные, - можно, причем начинать можно с любой точки;
- если нечетных вершин ровно две - тоже можно, но начинать и заканчивать надо только в нечетных вершинах;
- во всех остальных случаях - нельзя.
Используя правило, видим, что сделать рисунок, не отрывая руки и не повторяя ни одной линии
а) можно, так как нет нечетных вершин,
б) можно, так как нечетных вершины две,
в) нельзя, так как нечетных вершин четыре.
Вычислим площадь раскрашенной части.
Длина двух клеточек тетради составляет 1 см, значит квадратик из четырех клеточек имеет площадь 1 см².
Один коричневый треугольник занимает ровно половину от двух клеток. Два таких треугольника - две клетки. А четыре треугольника - 4 клетки. Т.е.
площадь коричневого цвета 1 см².
Фиолетовый участок состоит из трех квадратов, по 4 клетки каждый, т.е. 3 см², и двух треугольников. Один треугольник имеет площадь такую же, как два коричневых. Значит два треугольника - как 4 коричневых. Итак,
площадь фиолетового цвета составляет 4 см².