Математика, вопрос задал Viva8888 , 6 лет назад

Решите задачу. Даю 40

Приложения:

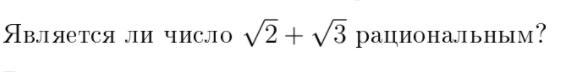
yugolovin: Если бы оно было рациональным, его квадрат, равный 5+2корня(6), тоже был бы рациональным, Но иррациональность корня из 6 доказывается стандартным способом

mvolturi: Здравствуйте!! Извините что отнимаю время. Я плаваю в аркфункциях, болел и пропустил эту тему в школе((( Если Вам не трудно, не могли бы помочь с моими заданиями? Я буду очень признателен. Я бы и сам попытался, но увы, не знаю с чем есть эти функции.

Ответы на вопрос

Ответил yugolovin

Ес ли бы число $\sqrt{2}+\sqrt{3}$ было рациональным, то и число

$(\sqrt{2}+\sqrt{3})^2=2+3+2\sqrt{6}=5+2\sqrt{6}$ было рациональным, а тогда и

$2\sqrt{6},$ а за ним и $\sqrt{6}$ было бы рациональным. Докажем, что это не так.

Если $\sqrt{6}=\dfrac{m}{n}\Rightarrow 6=\dfrac{m^2}{n^2};\ m^2=6n^2.$ Правая часть делится на 6, поэтому левая часть также делится на 6, а тогда и m делится на 6, m=6k;

36k²=6n²; 6k²=n²⇒ n² делится на 6 ⇒ n делится на 6. Но мы могли с самого начала. сократив дробь, считать, что m и n взаимно просты. Полученное противоречие доказывает утверждение

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Русский язык, 1 год назад

что называют словом деревня...

Математика, 1 год назад

ВЫЧИСЛИТЕ ЗНАЧЕНИЕ ВЫРАЖЕНИЯ 1)(3/4+3/8+5/6)*24= 2)7*2/3+7*1/2+7*5/6=...

Русский язык, 6 лет назад

10. Найди орфаграммы Каждый народ имеет свой дорогой и родной ему язык. У разных народов языки разные, но везде выступают как средство общения, без которого не может быть такого че- ловеческого...

Русский язык, 6 лет назад

можете придумать вопросительное предложение, но с прямой речью на середине. Типо „а,“п, „ продолжение слова автора(?)“ п это прямая речь, а - а это слова автора. Заранее благодарю...

Математика, 8 лет назад

На двух островках сидело 105 чаек, на одном из них было на 13 чаек больше, чем на втором. Сколько чаек сидело на каждом островке...

Литература, 8 лет назад

Срочно помогите!!! Какие у Герасима эмоции поступки...