Математика, вопрос задал penguinmen , 9 лет назад

Решите В14.В14Найдитенаибольшеезначениефункции 3x5 20x3 54 наотрезке [4;1].

Приложения:

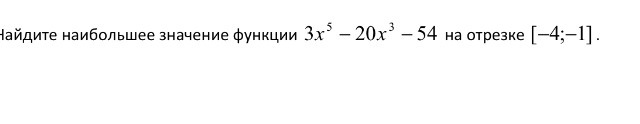
Ответы на вопрос

Ответил Trover

$f(x)=3x^5-20x^3-54\f'(x)=15x^4-60x^2=15x^2(x^2-4)\f'(x)=0Rightarrow15x^2(x^2-4)=0\15x^2=0Rightarrow x=0\x^2-4=0Rightarrow x^2=4Rightarrow x=-2,quad x=2$

Отрезку [-4, -1] принадлежит только точка -2. Вычислим значения функции в этой точке и на концах отрезка:

$f(-4) = 3(-4)^5-20(-4)^3-54=3(-1024)-20(-64)-54=-3072+1280-54=-1846\f(-2)=3(-2)^5-20(-2)^3-54=3(-32)-20(-8)-54=-96+160-54=10\f(-1)=3(-1)^5-20(-1)^3-54=-3+20-54=-37$

Выходит, что на отрезке [-4, -1] при x=-4 функция имеет наименьшее значение -1846, при x=-2 - наибольшее 10.

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Информатика, 6 лет назад

5. Напишите программу вычисления площади круга, если известна известна Длина окружности.

Қазақ тiлi, 6 лет назад

дам 50 б срочно !!!!!!!

Математика, 9 лет назад

Матэматыка 4*x-x+6*x-34=83...

Математика, 9 лет назад

Сколько сможете решить ) Задача. В правильной четырехугольной пирамиде со стороной основания, равной боковому ребру, найдите угол между стороной основания и скрещивающимся с ней боковым ребром.

Геометрия, 9 лет назад

Дано: треугольник ABC-прямоугольный. угол С=90 градусов. угол А=а, ВС=а. СD перпендикулярно АВ. найти СD.

Алгебра, 9 лет назад

ОБЪЯСНИТЕ!!!! линейные уравнение 3х+ 4у=2 И ВООБЩЕ ЛИНЕЙНЫЕ УРАВНЕНИЯ ТАКИЕ...