Решите уравнение ПЖ!!!
4sin^2*x+sinx*cosx-3*cos^2*x=0
Ответы на вопрос
Ответил asmitina2015
1
Ответ:
смотри в закрепе и пиши, если что-то непонятно, отвечу сразу
Пошаговое объяснение:
4sin^2 2x+ sinx*cosx-3cos^2 x= 0
8sinx*cosx+sinx*cosx-3cos^2x=0
9 sinx*cosx-3cos^2x=0( все разделим на 3)
3sinx*cosx-cos^2x=0
cosx(3sinx-cosx)=0
cosx=0
x= pi\2+pi*n, n принадлежит z
или 3sinx-cosx=0(разделим на cosx)
3tgx-1=0
tgx=1\3
x= arctg1\3+pi*k, kпринадлежит z
Приложения:
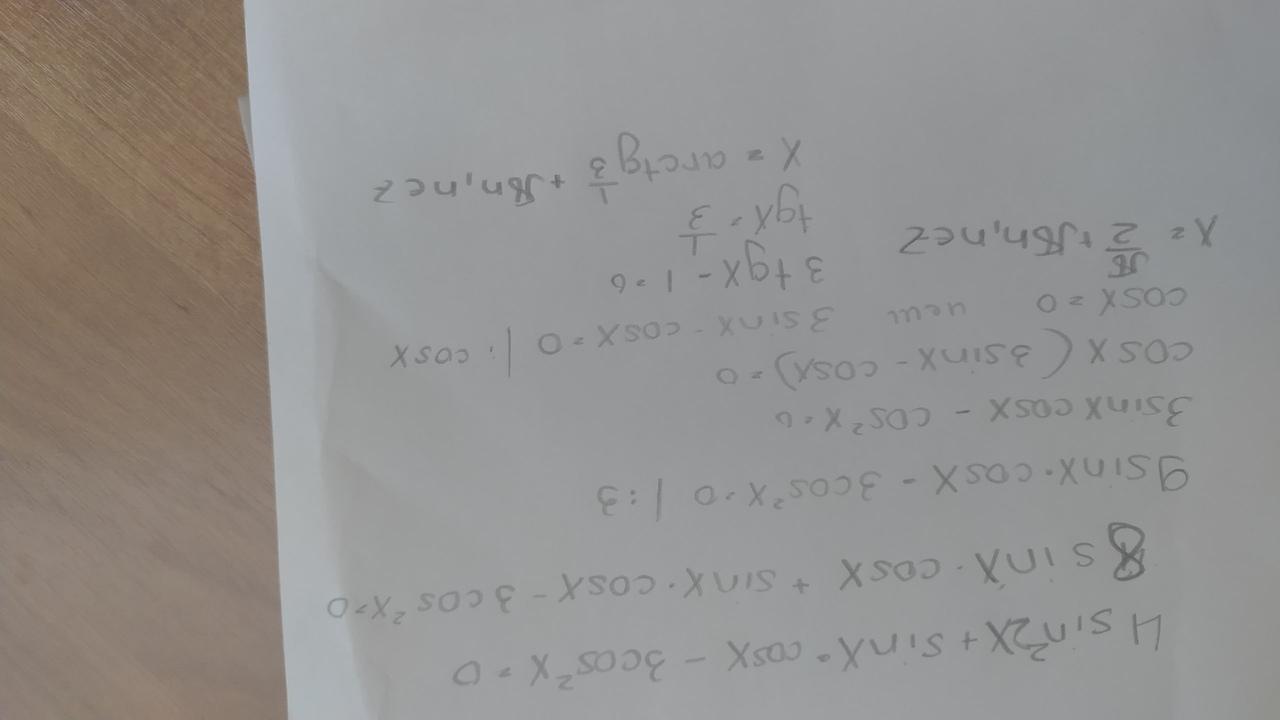
stasxstas2001:
Привет
У меня в начале 4sin^2*x а не синус двойного угла!
тогда еще легче: выводишь косинус квадрат равняется единица минус синус квадрат, находишь подобные, выносишь синус за скобки, если произведние ноль, значит либо одна часть ноль либо другая, если синус x равняется нулю то x равняется пи умножить на н, где н принадлежит зет, вторая часть тоже ноль, там арксинус получится
можешь на фото также
Лучшая
Новые вопросы
Українська мова,
1 год назад
Русский язык,
1 год назад
Алгебра,
2 года назад
Английский язык,
2 года назад
Математика,
7 лет назад