Алгебра, вопрос задал Vika7088708 , 8 лет назад

решите уравнение по алгебре

Приложения:

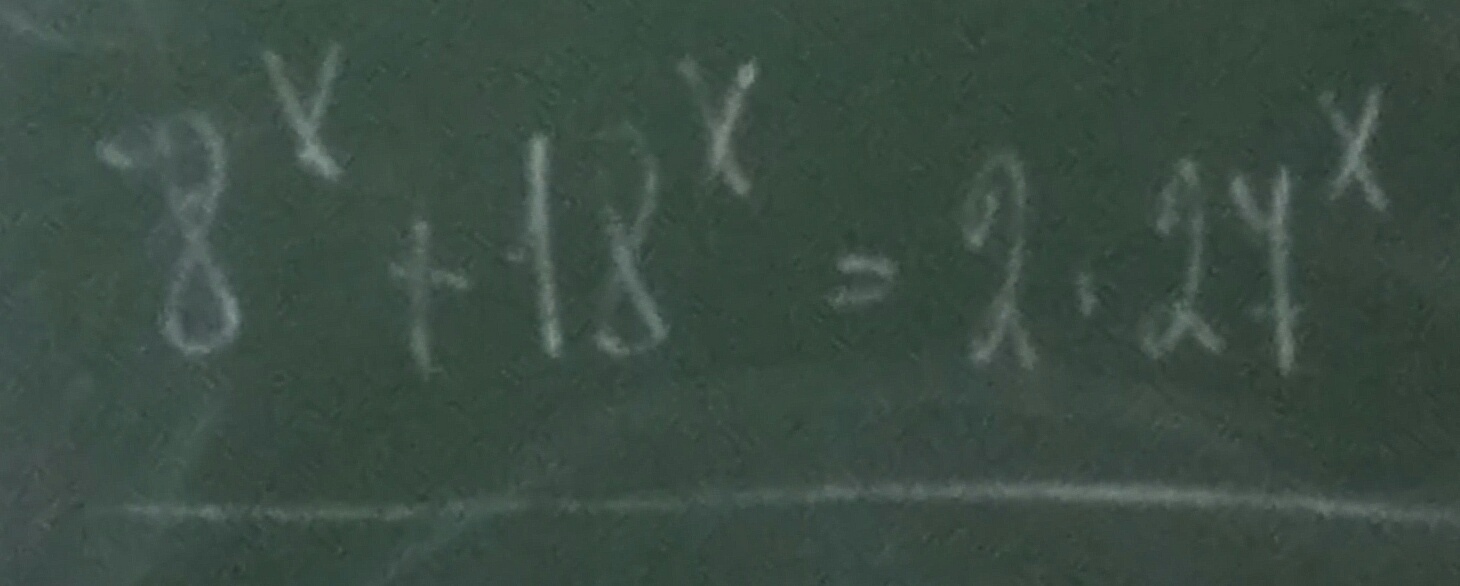
Ответы на вопрос

Ответил yugolovin

$8^x+18^x=2cdot 27^x; 2^{3x}+2^xcdot 3^{2x}-2cdot 3^{3x}; 2^x=p textgreater 0; 3^x=q textgreater 0;$

$p^3+pq^2-2q^3=0; left(frac{p}{q}right)^3+frac{p}{q}-2=0; frac{p}{q}=t textgreater 0;$

$t^3+t-2=0;$ угадываем t=1, делим многочлен, стоящий в левой части уравнения, на (t-1) (столбиком или устно):

$(t-1)(t^2+t+2)=0$ ; дискриминант квадратного трехчлена меньше нуля, поэтому единственное решение t=1; p=q; $left(frac{2}{3}right)^x=1; x=0$

Второй способ. Делим уравнение на $27^x; left(frac{2}{3}right)^{3x}+left(frac{2}{3}right)^x=2;$ угадываем x=0, после чего ссылаемся на то, что левая часть убывает, а правая постоянна. Это говорит о том, что других решений нет.

Ответ: 0

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Другие предметы, 2 года назад

Помогите! Нужно срочно!

Французский язык, 2 года назад

помогите пожалуйста умоляю...

Литература, 8 лет назад

Синонимы к слову унылый...

Обществознание, 8 лет назад

Гражданин Российской Федерации должен, Напишите срочно 5 пунктов что он должен!

Химия, 9 лет назад

ЗАДАЧА вычислите количество вещества, соответствующее 4,9 г. фосфорной кислоты...

История, 9 лет назад

каковы непосредственные причины Медного и Соляного бунтов ?