Решите уравнение (фото прикреплено)
Приложения:
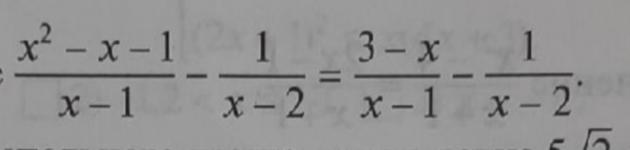
mathgenius:
x^2 - 4 =0. ОДЗ: x не равен 1 и не равен 2(главный подводный камень). x^2 = 4; x = -2. Ответ: x = - 2
Нельзя уничтожать член 1/(x-2) не записав ОДЗ. Имейте это ввиду
Ответы на вопрос
Ответил ninjazhanibek
1
(x²-4)/(x-1)=0
x²-4=0
x²=4
x=±√4=±2
Учитывая ОДЗ х-1≠1 и х-2≠2 ⇒ х≠1 и 2
тогда единственный корень -2
Ответ: -2
Ответил nessymirrey1
0
Ответ:
Объяснение:
группировка по разным знаменателям, при "х" ≠ 1; х ≠ 2
ограничения
ответ;
Новые вопросы