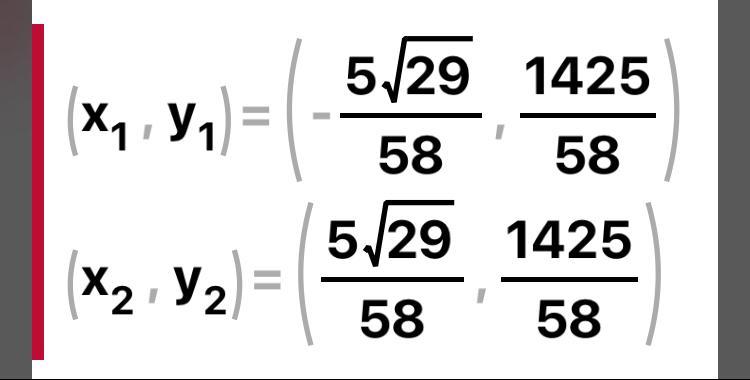Решите уравнение: 2x^2+y=23 10x^2-y=25
Ответы на вопрос
Ответ:
x1 = -sqrt(1154)*(im(y)^2 + re(y)^2)^(1/4)*cos(atan2(im(y, re(y))/2)/1154 - i*sqrt(1154)*(im(y)^2 + re(y)^2)^(1/4)*sin(atan2(im(y), re(y))/2)/1154)
x2 = sqrt(1154)*(im(y)^2 + re(y)^2)^(1/4)*cos(atan2(im(y, re(y))/2)/1154 + i*sqrt(1154)*(im(y)^2 + re(y)^2)^(1/4)*sin(atan2(im(y), re(y))/2)/1154)
Объяснение:
_________________ _________________
______ 4 / 2 2 /atan2(im(y), re(y)) ______ 4 / 2 2 /atan2(im(y), re(y))
/ 1154 */ im (y) + re (y) *cos|-------------------| I*/ 1154 */ im (y) + re (y) *sin|-------------------|
2 / 2 /
x1 = - ------------------------------------------------------ - --------------------------------------------------------
1154 1154
_________________ _________________
______ 4 / 2 2 /atan2(im(y), re(y)) ______ 4 / 2 2 /atan2(im(y), re(y))
/ 1154 */ im (y) + re (y) *cos|-------------------| I*/ 1154 */ im (y) + re (y) *sin|-------------------|
2 / 2 /
x2 = ------------------------------------------------------ + --------------------------------------------------------
1154 1154