Математика, вопрос задал dandy68 , 2 года назад

решите срочно пожалуйста!!

Приложения:

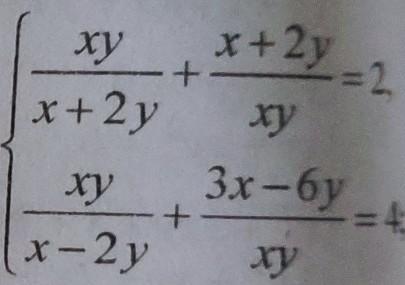
ВикаБач: В 1 уравнении сумма взаимно-обратных чисел =2, это возможно лишь если 1+1=2, значит ху=х+2у

Ответы на вопрос

Ответил MatemaT123

Ответ:

$(6; \quad 1,5)$

Пошаговое объяснение:

ОДЗ:

$x \neq 0, \quad y \neq 0;$

$x \pm 2y \neq 0 \Rightarrow \frac{x}{y} \neq \mp 2;$

Решение:

$\left \{ {{\frac{xy}{x+2y}+\frac{x+2y}{xy}=2} \atop {\frac{xy}{x-2y}+\frac{3x-6y}{xy}=4}} \right. ;$

$t=\frac{xy}{x+2y} \Rightarrow \frac{x+2y}{xy}=\frac{1}{t};$

$t+\frac{1}{t}=2;$

$t^{2}+1=2t;$

$t^{2}-2t+1=0;$

$(t-1)^{2}=0;$

$t-1=0;$

$t=1 \Rightarrow \frac{xy}{x+2y}=1 \Rightarrow xy=x+2y;$

$k=\frac{xy}{x-2y} \Rightarrow \frac{x-2y}{xy}=\frac{1}{k} \Rightarrow \frac{3(x-2y)}{xy}=\frac{3}{k};$

$k+\frac{3}{k}=4;$

$k^{2}+3=4k;$

$k^{2}-4k+3=0;$

$1-4+3=-3+3=0 \Rightarrow k_{1}=1, \quad k_{2}=3:1=3;$

$k_{1}=1 \quad \vee \quad k_{2}=3 \Rightarrow \frac{xy}{x-2y}=1 \quad \vee \quad \frac{xy}{x-2y}=3 \Rightarrow xy=x-2y \quad \vee$

$\vee \quad xy=3(x-2y);$

$\left \{ {{xy=x+2y} \atop {xy=x-2y}} \right. \vee \left \{ {{xy=x+2y} \atop {xy=3(x-2y)}} \right. \Leftrightarrow \left \{ {{xy=x+2y} \atop {x+2y=x-2y}} \right. \vee \left \{ {{xy=x+2y} \atop {x+2y=3(x-2y)}} \right. \Leftrightarrow \left \{ {{xy=x+2y} \atop {2y+2y=x-x}} \right. \vee$

$\vee \left \{ {{xy=x+2y} \atop {6y+2y=3x-x}} \right. \Leftrightarrow \left \{ {{xy=x+2y} \atop {4y=0}} \right. \vee \left \{ {{xy=x+2y} \atop {8y=2x}} \right. \Leftrightarrow \left \{ {{xy=x+2y} \atop {y=0}} \right. \vee \left \{ {{xy=x+2y} \atop {x=4y}} \right. \Leftrightarrow \left \{ {{x=0} \atop {y=0}} \right. \vee$

$\vee \left \{ {{4y^{2}=4y+2y} \atop {x=4y}} \right. ;$

Первая пара корней не удовлетворяет ОДЗ, поэтому перейдём к решению второй пары уравнений:

$\left \{ {{4y^{2}=4y+2y} \atop {x=4y}} \right. \Leftrightarrow \left \{ {{4y^{2}=6y} \atop {x=4y}} \right. \Leftrightarrow \left \{ {{4y^{2}-6y=0} \atop {x=4y}} \right. \Leftrightarrow \left \{ {{y(4y-6)=0} \atop {x=4y}} \right. \Leftrightarrow \left \{ {{y=0} \atop {x=4y}} \right. \vee \left \{ {{4y-6=0} \atop {x=4y}} \right. \Leftrightarrow$

$\Leftrightarrow \left \{ {{x=0} \atop {y=0}} \right. \vee \left \{ {{4y=6} \atop {x=4y}} \right. \Leftrightarrow \left \{ {{x=0} \atop {y=0}} \right. \vee \left \{ {{x=6} \atop {y=1,5}} \right. ;$