Решите систему уравнений.
Приложения:
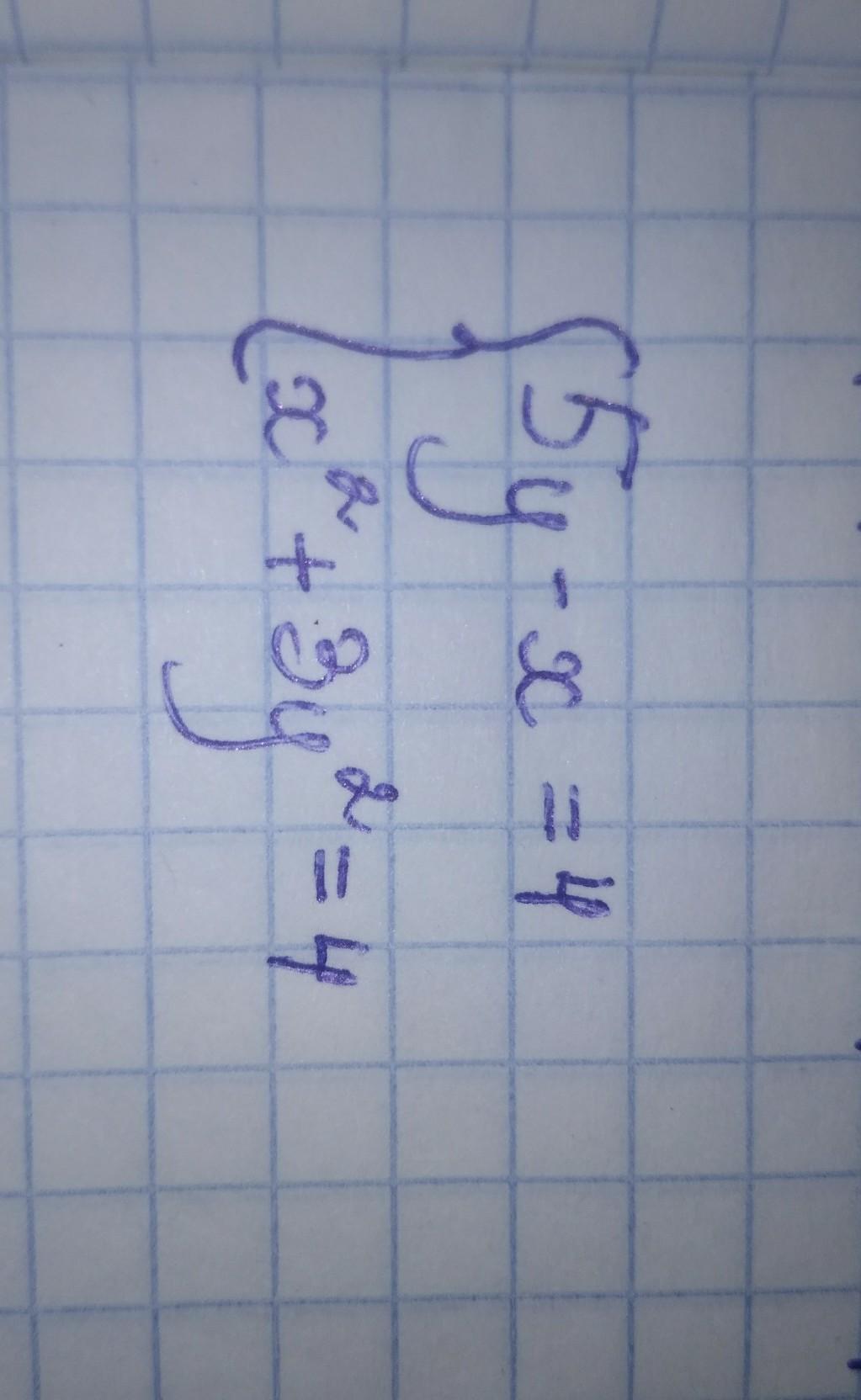
Ответы на вопрос
Ответил slganiev
1
Ответ:
х1=-13/7, х2=1 у1=3/7 у2=1
Объяснение:
х=5у-4
(5у-4)²+3у²=4
14у²-20у+6=0
7у²-10у+3=0 знайдемо дискриминант і корені рівняння D=4
у1=3/7 у2=1 знайдемо х1=5*3/7-4=-13/7 х2=5*1-4=1
Ответил prokhpav
1
Ответ:
Объяснение:
Выразим через верхнее уравнение x:
Подставим значение x во второе уравнение:
Получается обычное квадратное уравнение. Для удобства сократим его на 4:
Подбираем такие числа a и b, что ab=7*3 и a+b=-10. Это числа -7 и -3. В соответствии с ними раскладываем -10y:
И раскладываем на множители:
Отсюда следует решение уравнения:
Вычисляем соответствующий х:
Новые вопросы