Алгебра, вопрос задал alberona02 , 7 лет назад

Решите систему уравнений:

Приложения:

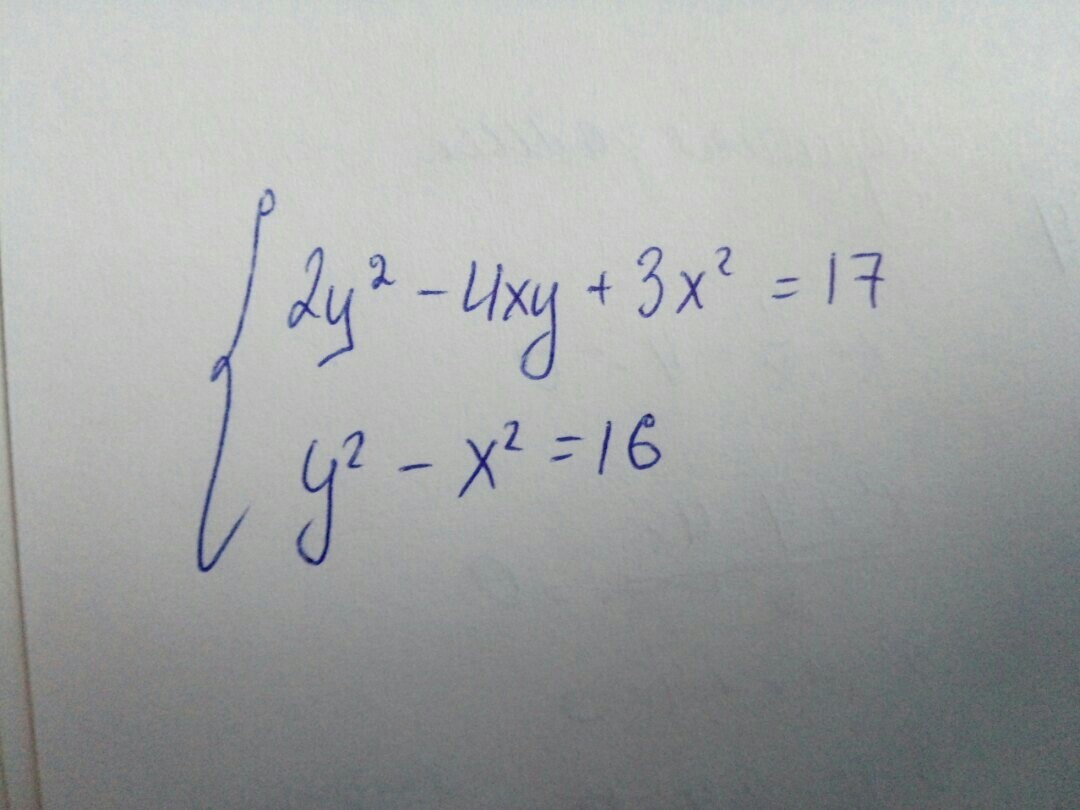
Ответы на вопрос

Ответил DNHelper

Заметим, что 17 = 16 + 1 ⇒ 2y² - 4xy + 3x² = y² - x² + 1 ⇔ y² - 4xy + 4x² = 1 ⇔ (y - 2x)² = 1 ⇒ y = 2x + 1 или y = 2x - 1.

$left { {{y=2x+1} atop {(2x+1)^2-x^2=16}} right. \ left { {{y=2x+1} atop {3x^2+4x-15=0}} right. \left { {{y=2x+1} atop {x=-3; frac{5}{3}}} right. \ left { {{x=-3} atop {y=-5}} right. left { {{x=frac{5}{3}} atop {y=frac{13}{3}}} right.$ или $left { {{y=2x-1} atop {(2x-1)^2-x^2=16}} right. \left { {{y=2x-1} atop {3x^2-4x-15=0}} right. \ left { {{y=2x-1} atop {x=-frac{5}{3}; 3}} right. \ left { {{x=-frac{5}{3}} atop {y=-frac{13}{3}}} right. left { {{x=3} atop {y=5}} right.$

Ответ: $(-3; -5), (-frac{5}{3}; -frac{13}{3}), (frac{5}{3}; frac{13}{3}), (3; 5)$

Ответил AntVa

еще раз привет, если решив уравнение вторым, а значит позже чем первый, видишь что первое не верное, то проверив, точно ли не верно решено первый отвечающим - жми отметить нарушение: "не верный ответ", тоже про спам, плагиат, рекламу и прочие не хорошести!

Ответил DNHelper

Я не помню, чтобы тут было какое-то второе решение. Но если это просто совет, то спасибо!

Ответил AntVa

конечно совет :)

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Русский язык, 1 год назад

Закончите начатые фразы подходящими словарными словами из списка, ставя их в нужной форме. Вставьте пропущенные буквы. 1. Болезненный, тяжёлый сон называют ... 2. В освоении космоса у...

Русский язык, 1 год назад

Образуйте существительные со значением "профессия". 1.Тот,то учитывает работу.2. Тот,кто изучает историю.3.Тот,кто пилит дрова.4.Тот,кто чинит водопровод.5.Тот,кто переводит книги с иностранного...

Биология, 7 лет назад

Листорасположение волжанки?

Литература, 7 лет назад

Пж срочно.срочно! Плиз...

Геометрия, 8 лет назад

Решите пожалуйста срочно !!!

Литература, 8 лет назад

рассказ про дружбу для чтения что бы он был маленький и интересный...