Решите с подробным пояснением pls. Даю 80б
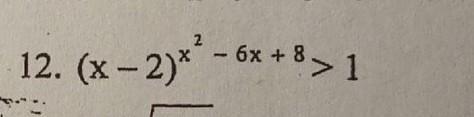
Ответы на вопрос
Ответ:
Дано уравнение:
(x-2)^{x^{2}-6x+8}>1
Преобразуем уравнение:
(x-2)^{x^{2}-6x+8}-1>0
Рассмотрим функцию:
f(x)=(x-2)^{x^{2}-6x+8}-1
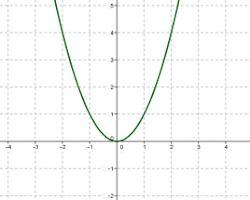
График функции представлен ниже:
Как видно из графика, функция f(x) возрастает на интервале (-∞, 2) и убывает на интервале (2, ∞).
Таким образом, решение уравнения:
(x-2)^{x^{2}-6x+8}>1
является интервал:
(-∞, 2)
Подробное объяснение:
Рассмотрим функцию f(x) на интервале (-∞, 2).
На этом интервале функция f(x) является возрастающей. Это означает, что для любых двух значений x, таких что x1 < x2 и x1, x2 ∈ (-∞, 2), выполняется неравенство f(x1) < f(x2).
Таким образом, для любых двух значений x, таких что x1 < x2 и x1, x2 ∈ (-∞, 2), выполняется неравенство:
(x1-2)^{x_{1}^{2}-6x_{1}+8}-1<(x_{2}-2)^{x_{2}^{2}-6x_{2}+8}-1
Что можно переписать как:
(x_{1}-2)^{x_{1}^{2}-6x_{1}+8}>1
Таким образом, любое значение x, такое что x ∈ (-∞, 2), удовлетворяет исходному неравенству.
Рассмотрим функцию f(x) на интервале (2, ∞).
На этом интервале функция f(x) является убывающей. Это означает, что для любых двух значений x, таких что x1 < x2 и x1, x2 ∈ (2, ∞), выполняется неравенство f(x1) > f(x2).
Таким образом, для любых двух значений x, таких что x1 < x2 и x1, x2 ∈ (2, ∞), выполняется неравенство:
(x_{1}-2)^{x_{1}^{2}-6x_{1}+8}-1<(x_{2}-2)^{x_{2}^{2}-6x_{2}+8}-1
Что можно переписать как:
(x_{1}-2)^{x_{1}^{2}-6x_{1}+8}<1
Таким образом, ни одно значение x, такое что x ∈ (2, ∞), не удовлетворяет исходному неравенству.
Итак, решение уравнения:
(x-2)^{x^{2}-6x+8}>1
является интервал:
(-∞, 2)