Решите с Дано пожалуйста или просто решите
Приложения:
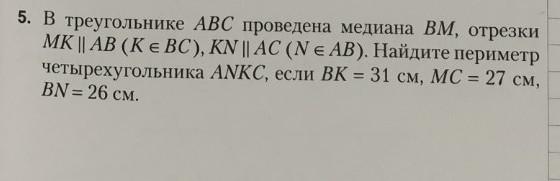
Ответы на вопрос
Ответил Medved23
1
Объяснение: рисунок к задаче прилагаю.
Дано: ΔABC, т. M ∈ AC (AM = CM), т. K ∈ BC, т. N ∈ AB;
MK || AB, KN || AC, BK = 31 см, MC = 27 см, BN = 26 см.
Найти: .
Решение. Сразу найдем сторону AС. ВМ - медиана ⇒ AС = 2МС = 54 см.
Докажем, что NK - средняя линия треугольника АВС.
Поскольку MK || AB и KN || AC, то четырехугольник AMKN - параллелограмм. А это значит, что NK = AM = 1/2 AC = 27 см ⇒ NK - средняя линия треугольника по определению ⇒ BN = AN = 26 см, BK = KC = 31 см.
Ищем периметр: = AN + NK + KC + AC = 26 + 27 + 31 + 54 = 138 см.
ОТВЕТ: 138.
Приложения:
Ответил Аноним
1
решение. рисунок. данные и ответ во вложении
Приложения:

Новые вопросы