Решите производные......................
Приложения:

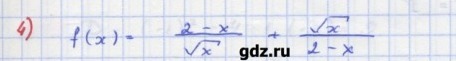
Ответы на вопрос
Ответил NNNLLL54
0
Igor171717:
объясните предпоследнюю строчку =(
В числителях раскрыли скобки. Затем упростили выражение, вынесли общий множитель за скобку.
Как вы от сложения перешли к делению?
От сложения к умножению точнее.
Вынесла общий множитель. Им является числитель одной из дробей ( я выбрала числитель 1 дроби). Числитель 2 дроби тот же, что и у 1 дроби, только с противоположным знаком.
Новые вопросы
Информатика,
1 год назад
Русский язык,
1 год назад
Литература,
1 год назад
Биология,
7 лет назад
Экономика,
7 лет назад