Решите пожалуйста , завтра уже сдавать, здесь легко!!!!номера :
72,74
Приложения:
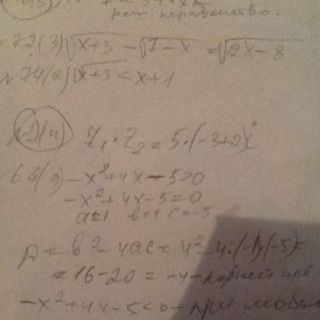
Ответы на вопрос
Ответил mefody66
0
72) Если я правильно понял
√(x+3) - √(7-x) = √(2x-8)
Во-первых, область определения
x >= -3, x <= 7, x >= 4
x принадлежит [4, 7]
Возводим в квадрат
x + 3 + 7 - x - 2√((x+3)(7-x)) = 2x - 8
2√((x+3)(7-x)) = 10 + 8 - 2x = 18 - 2x
√((x+3)(7-x)) = 9 - x
Возводим в квадрат
7x + 21 - x^2 - 3x = (9 - x)^2 = x^2 - 18x + 81
2x^2 - 22x + 60 = 0
x^2 - 11x + 30 = 0
(x - 5)(x - 6) = 0
x1 = 5, x2 = 6
Оба подходят под область определения.
74) √(x + 3) < x + 1
Область определения x >= -3
Возводим в квадрат
x + 3 < x^2 + 2x + 1
Система
{ x^2 + x - 2 > 0
{ x >= -3
{ (x - 1)(x + 2) > 0
{ x >= -3
x принадлежит [-3, -2) U (1, +oo)
√(x+3) - √(7-x) = √(2x-8)
Во-первых, область определения
x >= -3, x <= 7, x >= 4
x принадлежит [4, 7]
Возводим в квадрат
x + 3 + 7 - x - 2√((x+3)(7-x)) = 2x - 8
2√((x+3)(7-x)) = 10 + 8 - 2x = 18 - 2x
√((x+3)(7-x)) = 9 - x
Возводим в квадрат
7x + 21 - x^2 - 3x = (9 - x)^2 = x^2 - 18x + 81
2x^2 - 22x + 60 = 0
x^2 - 11x + 30 = 0
(x - 5)(x - 6) = 0
x1 = 5, x2 = 6
Оба подходят под область определения.
74) √(x + 3) < x + 1
Область определения x >= -3
Возводим в квадрат
x + 3 < x^2 + 2x + 1
Система
{ x^2 + x - 2 > 0
{ x >= -3
{ (x - 1)(x + 2) > 0
{ x >= -3
x принадлежит [-3, -2) U (1, +oo)
Новые вопросы