Решите пожалуйста, заранее спасибо
Приложения:
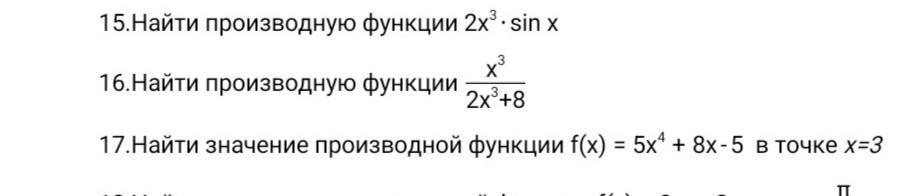
Ответы на вопрос
Ответил bahytgulkabylainova
1
Ответ:
1)=6хsinx+2x^3cosx=2x(3sinx+x^2cosx)
2)(x^3)'(2x^3+8)-x^3(2x^3+8)'/(2x^3+8)^2=
3x^2(2x^3+8)-x^3×6x^2/(2x^3+8)^2=
2x^5+8x^2-6x^5/(2x^3+8)^2
8x^2-5x^5/(2x^3+8)^2=
x^2(8-5x^3)/(2x^3+8)^2
3)f'(x)=20x^3+8
f'(3)=20×27+8=548
Ответил Tkinter
0
Ответ:
Пошаговое объяснение:
15. y'(x)= (2x³)'·sinx + 2x³ · >(sinx)' = 6x²·sinx + 2x³·cosx
16. y'(x) = [ (x³)' ·(2x³+8) -x³· (2x³+8)' ] / (2x³+8)²]= [3x²·(2x³+8) - x³ ·6x²]/ (2x³+8)²] = (2x³+8) /(2x³+8)² = 1/(2x³+8).
17. y'(x) = 20x³ +8 ⇔ y'(3) = 20·27 +8 = 548.
Новые вопросы
Математика,
1 год назад
Русский язык,
1 год назад
Математика,
6 лет назад
Математика,
8 лет назад
Биология,
8 лет назад