Решите пожалуйста задачу с фотографии.

Ответы на вопрос
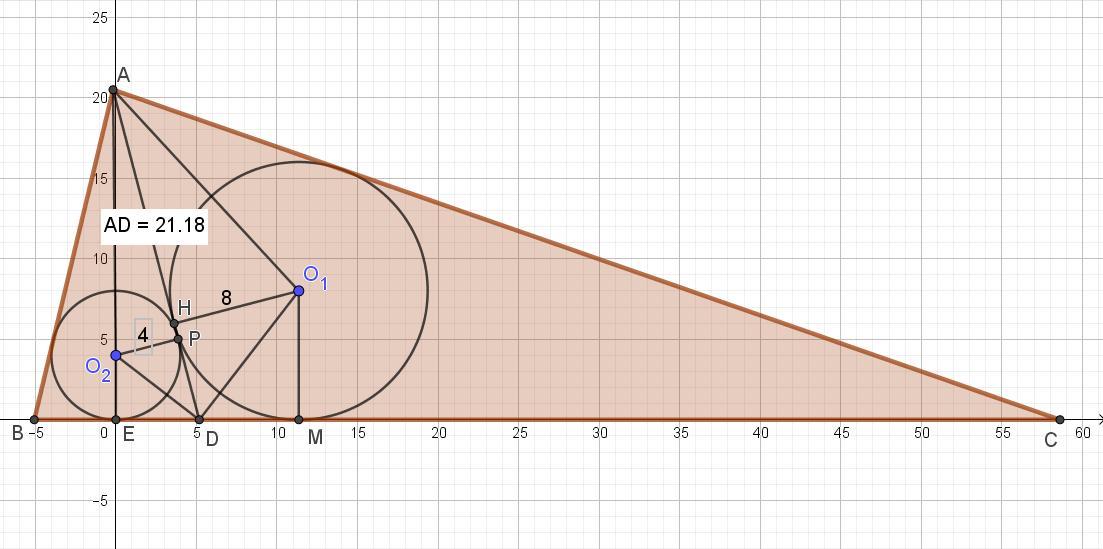
AD - общая касательная двух окружностей. ЕМ = √129.
Поэтому угол О2ДЕ равен углу ДО1М как половины равных взаимно перпендикулярных углов.
Используем равенство тангенсов этих углов. Пусть ЕД = в.
4/в = ДМ/8. Заменим ДМ = (√129) - в.
4/в = ((√129) - в)/8,
32 = √129*в - в². Получили квадратное уравнение:
в² - √129*в + 32 = 0. Д = 129 - 4*32 =129 - 128 = 1.
в1 = (√129 - 1 )/2, в2 = (√129 + 1 )/2.
Собственно в1 = ЕД, а в2 = ДМ, так как вы сумме равны ЕМ = √129.
По свойству касательной ЕД = ДР = ((√129 - 1 )/2) ≈ 5,18.
Отрезок РН равен 1 как разность ЕД и ДМ.
Теперь перейдём к рассмотрению половин заданных углов.
Примем отрезок РА = х.
tg(О2РА) = 4/х, tg(О1НА) = 8/(х - 1).
В соответствии с заданием угол О1НА равен двум углам О2РА = α.
Используем формулу двойного угла: tg 2α = 2tg α/(1 - tg²α).
Подставим значение tg α = 4/х.
tg 2α = (2*(4/х))/(1 - 16/х²) = 8х/(х² - 16).
Приравняем полученное значение ранее определённому.
8х/(х² - 16) = 8/(х - 1),
8х² - 8х = 8х² - 128,
8х = 128,
х = 128/8 = 16. Это длина отрезка АР.
Отсюда ответ: АД = АР + ДР = 16 + (((√129) - 1 )/2) = (31 + √129)/2.
Это значение примерно равно 21,18.