Решите пожалуйста задачи.
1).
В равнобедренном треугольнике ABC с основанием АС проведена биссектриса BD.
Докажите что точка М, взятая на этой биссектрисе, равноудалена от вершин А и С.
2)
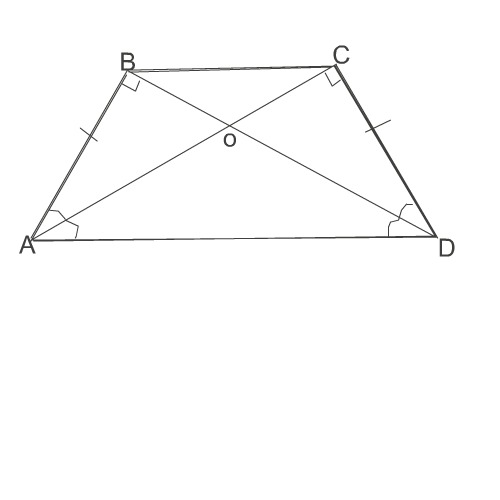
В рпвнобедренной трапеции диагональ перпендикулярно боковой стороне и является биссектрисой одного из углов трапеции. В каком отношении диагонали трапеции делятся точкой их пересечения?
Ответы на вопрос
1)
Так как треугольник равнобедренный, биссектриса в нем "3 в одном флаконе": биссектриса, высота и медиана. Медиана делит сторону, к которой проведена, на две равные части.
Следовательно, АD=DC.
2)
Пусть это трапеция АВСD. Нужно найти ВО:ОD
Так как АВ=СD, то
∠ АВD=∠ АСD
Сравним треугольник АВD и АВО
В них, как в любом треугольнике, сумма углов 180º.
В треугольнике АВD
сумма углов равна
180º=90º + ∠А+∠А:2 ( так как ∠А=∠D)
В треугольнике АВО
180º=90º+∠А:2+ ∠АОВ
Следовательно, ∠АОВ = ∠А
∠А+∠А:2=180º-90º=90º
1,5 ∠А=90º
0,5∠А=30º
∠ВАО=30º По свойству катета, противолежащего углу 30º
ВО=АО:2
АО=ОD
ВО:ОD=1:2