Алгебра, вопрос задал ireena , 1 год назад

Решите, пожалуйста, уравнения с корнями(иррациональные уравнения.)

Приложения:

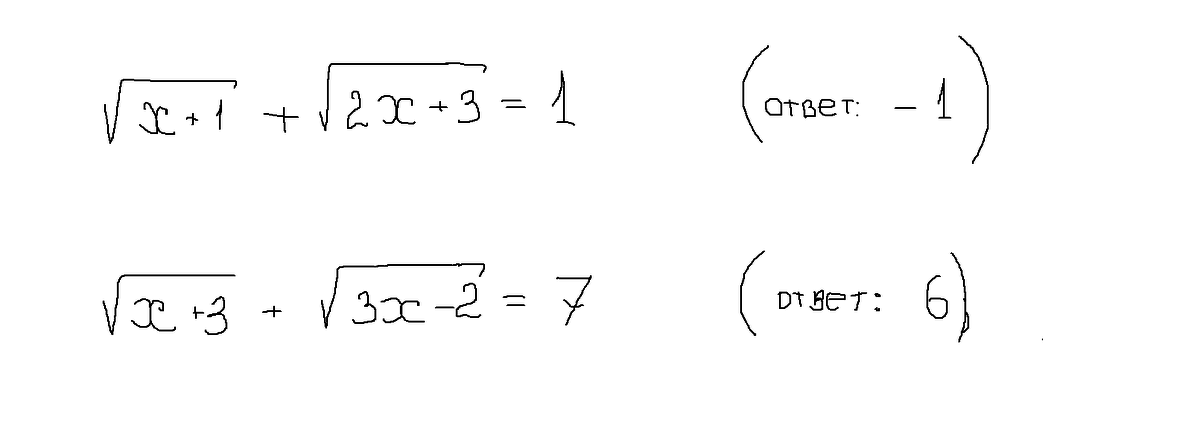
Ответы на вопрос

Ответил mukus13

$\sqrt{x+1}+ \sqrt{2x+3} =1$

ОДЗ:
$\left \{ {{x+1 \geq 0} \atop {2x+3 \geq 0}} \right.$

$\left \{ {{x \geq -1} \atop {x \geq -1.5} \right.$

$x$ ∈ $[-1;+$ ∞ $)$

$(\sqrt{x+1}+ \sqrt{2x+3})^2 =1^2$

$x+1+2x+3+2 \sqrt{(x+1)(2x+3)} =1$

$2 \sqrt{(x+1)(2x+3)} =-3x-3$

$-3x-3 \geq 0$
$x \leq -1$

$4(2 x^{2} +3x+2x+3)=9 x^{2} +9+18x$

$8 x^{2} +20x+12=9 x^{2} +9+18x$

$x^{2} -2x-3=0$

$D=4+12=16$
$x_1=-1$
$x_2=3$ не подходит

Ответ: $-1$

№ 2
$\sqrt{x+3} + \sqrt{3x-2} =7$

ОДЗ:
$\left \{ {{x+3 \geq 0} \atop {3x-2 \geq 0}} \right.$

$\left \{ {{x \geq -3} \atop {x \geq \frac{2}{3} }} \right.$

$x$ ∈ $[ \frac{2}{3} ;+$ ∞ $)$

$( \sqrt{x+3} + \sqrt{3x-2})^2 =7^2$

$x+3+3x-2+2 \sqrt{(x+3)(3x-2)} =49$

$2 \sqrt{(x+3)(3x-2)} =48-4x$

$\sqrt{(x+3)(3x-2)} =24-2x$

$24-2x \geq 0$
$-2x \geq -24$
$x \leq 12$

$( \sqrt{(x+3)(3x-2)})^2 =(24-2x)^2$

$(x+3)(2x-3)=576+4 x^{2} -96x$

$3 x^{2} -2x+9x-6=576+4 x^{2} -96x$

$x^{2} -103x+582=0$

$D=10609-2328=8281=91^2$
$x_1=6$
$x_2=97$ не подходит

Ответ: $6$

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Математика, 1 год назад

Упростить выражения 24y+7a-5a+8...

Русский язык, 1 год назад

6А. Кто такие путешественники-исследователи? Каких путе. шественников-исследователей вы знаете? Почему они отправ- лялись в путешествия? Одинаковы ли цели их путешествий и пу- тешествий современных...

Русский язык, 1 год назад

В каком ряду в произнесении терминов допущена ошибка? (1) антитЕза [тэ], оксЮморон (2) диОптрия, метонимИя (3) каучУк, лАзер [зэ] (4) апострОф, поликонденсАция [дэ]...

Английский язык, 1 год назад

КАКОЙ ВОПРОС СОСТАВЛЕН ПРАВИЛЬНО? 1)a)Who these girl are? b)Who are these girl? c)Who are these girls? d)Who is this girls? 2)a)Who read today? b)Who reads todae? c)Who do read today? d)Who...

Математика, 7 лет назад

Чему равен корень уравнения x-100=0...

Алгебра, 7 лет назад

Прямая L проходит через точку с координатами (-1:7) и пересекает график функции y=-4+x в точке с абсциссой x=1 Постройте график функции y=-4+x Постройте прямую L Задайте прямую L уравнением...