Алгебра, вопрос задал sasha54587 , 2 года назад

Решите пожалуйста уравнениепожалуйста даю 40 баллов

Приложения:

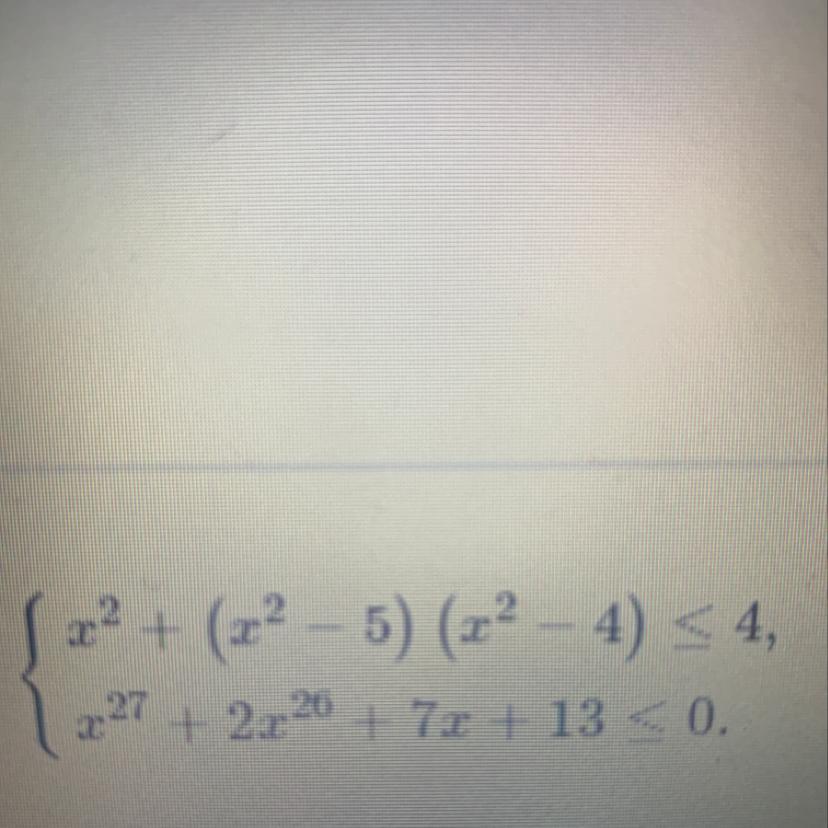
Ответы на вопрос

Ответил sangers1959
2

Объяснение:

\left \{ {x^2+(x^2-5)*(x^2-4)\leq 4} \atop {x^{27}+2*x^{26}+7x+13\leq 0}} \right. \\x^2-4+(x^2-5)*(x^2-4)\leq0\\ (x^2-4)*(1+x^2-5)\leq 0\\(x^2-4)*(x^2-4)\leq0\\ (x^2-4)^2\leq 0

Так как (x²-4)²≥0   ⇒

x^2-4=0\\(x+2)*(x-2)=0\\x_1=2;x_2=-2.

Подставляем корни первого неравенства во второе:

1) х=2.

2^{27}+2*2^{26}+2*7+13>0 \Rightarrow\\x= 2\notin.

2) x=-2.

(-2)^{27}+2(-2)^{26}+7(-2)+13=-2^{27}+2*2^{26}-14+13=-2^{27}+2^{27}-1=-1\Rightarrow \\x=-2\in.

Ответ: x=-2.

Предыдущий вопрос
Следующий вопрос
Новые вопросы