Алгебра, вопрос задал RIK777 , 2 года назад

решите пожалуйста систему, даю 30 балов

Приложения:

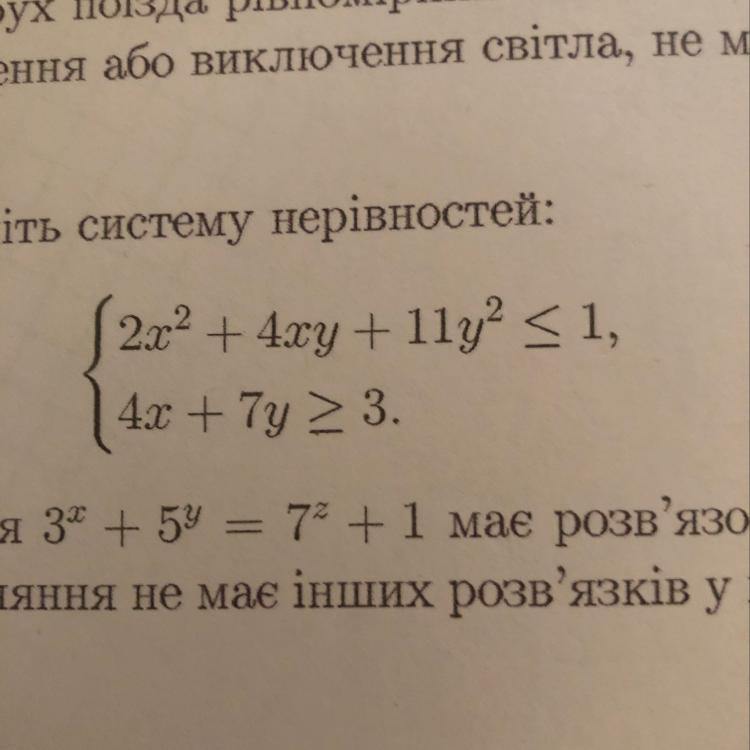
Ответы на вопрос

Ответил OneGyrus

Ответ: $(\frac{5}{9} ;\frac{1}{9} )$

Объяснение:

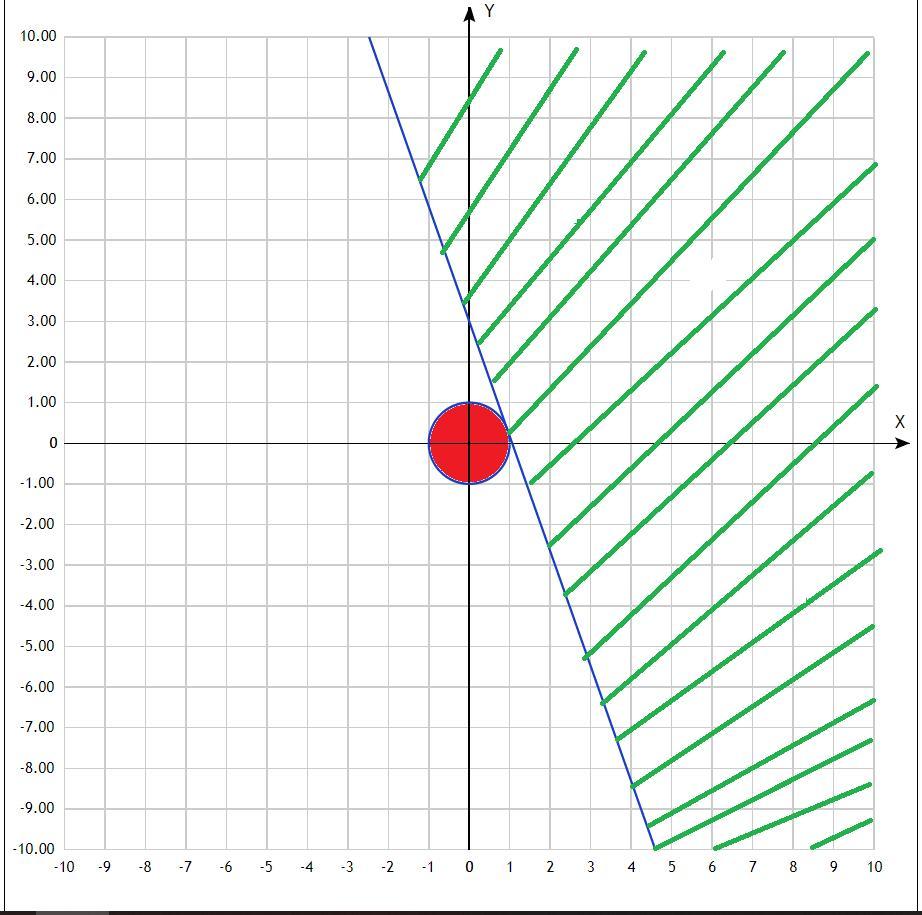
$\left \{ {{2x^2+4xy+11y^2\leq 1} \atop {4x+7y\geq 3}} \right.\\\left \{ {{2(x+y)^2 +(3y)^2\leq 1} \atop {4x+7y\geq 3}} \right.\\\sqrt{2} (x+y)=a\\3y=b\\ \left \{ {{a^2 +b^2\leq 1} \atop {2\sqrt{2}a +b \geq 3}} \right.\\$

Нарисуем в системе координат a,b область, указанную системой.

$a^2+b^2\leq1$ - представляет собой цельный круг радиуса $1$ в начале координат, включая окружность (красная заливка)

$2\sqrt{2}a+b\geq 3$ - это область НЕ НИЖЕ прямой $b= 3-2\sqrt{2}a$ (зеленая штриховка)

Определим в скольких точках данная прямая пересекается с окружностью, для этого подставим :

$b=3-2\sqrt{2}a \\a^2+( 3-2\sqrt{2} a)^2 = 1\\9a^2-12\sqrt{2}a +8 = 0\\\frac{D}{4} = 72-72 = 0\\a= \frac{6\sqrt{2} }{9} } = \frac{2\sqrt{2} }{3} }\\b = 3 - \frac{8}{3} =\frac{1}{3}$

Как видим, они имеют одну точку пересечения, иначе говоря, прямая касается окружности. Из рисунка видно, что решение системы это только данная точка пересечения.

Вернемся к замене:

$y=\frac{b}{3} =\frac{1}{9}\\x+y =\frac{a}{\sqrt{2} } = \frac{2}{3} \\x=\frac{2}{3} -\frac{1}{9} = \frac{5}{9}$

Приложения:

OneGyrus: Ответ исрпавлен, перезагрузи страницу

OneGyrus: исправлен*

RIK777: спасибо большое!

OneGyrus: не за что

OneGyrus: Есть еще тригонометрический способ: a=cos(t) ; |b|<=|sint| . Тогда из принципа вспомогательного аругемента:
2sqrt(2)a+b<= 2sqrt(2)*cos(t) +-sin(t) <= sqrt((2sqrt(2))^2+1^2) = sqrt(9) = 3

OneGyrus: То есть : 2sqrt(2)a+b<=3, но 2sqrt(2)a+b>=3 . Откуда: 2sqrt(2)a+b = 3 . Подставляем и решаем квадратное уравнение.

OneGyrus: Такая некая параметрическая замена

OneGyrus: Если есть желание, могу написать подробнее про этот способ.

RIK777: не, спасибо бро. ты очень помог и так!

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Английский язык, 1 год назад

Помогите пожалуйста и обьясните,так и так.ну просто обьясните,я не понимаю...

Русский язык, 1 год назад

помогите пожалуйстаа...

История, 2 года назад