Алгебра, вопрос задал polinamation , 6 лет назад

решите пожалуйста,очень срочно

Приложения:

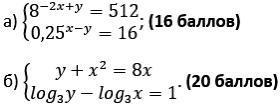
Ответы на вопрос

Ответил 1Hallo2

Ответ:

a) (-1; 1)

б) (5; 15)

Объяснение:

a) $\left \{ {{8^{-2x+y} =512} \atop {(\frac{1}{4})^{x-y} =16}} \right.\\\\8^{-2x+y} =512\\8^{-2x+y} =8^{3} \\-2x+y=3\\\\(\frac{1}{4})^{x-y} =16\\2^{-2(x-y)} =2^{4}\\-2x+2y=4\\-x+y=2\\\\\left \{ {{-2x+y=3} \atop {-x+y=2}} \right. \\\left \{ {{y=2x+3} \atop {y=x+2}} \right. \\\left \{ {{y=1} \atop {x=-1}} \right.$

б) $\left \{ {{y+x^2=8x} \atop {log(3)(y)-log(3)(x)=1}} \right. \\\\y+x^2=8x\\y=8x-x^{2}\\\\log(3)(y)-log(3)(x)=1\\log(3)(8x-x^{2})-log(3)(x)=log(3)(3)\\log(3)(\frac{x(8-x)}{x} )=log(3)(3)\\8-x=3\\x=5\\\\\left \{ {{y=8x-x^{2}} \atop {x=5}} \right. \\\left \{ {{y=8*5-25=15} \atop {x=5}} \right.$

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Русский язык, 1 год назад

здравствуйте,помогите пожалуйста.Выписать имена существительные и определить их род. Облако,...

Русский язык, 1 год назад

В одном из выделенных ниже слов допущена ошибка в образовании формы слова. Исправьте ошибку и запишите слово правильно. БОЛЕЕ ВЫСОКО расположен банка КОНСЕРВОВ в ТРЁХСТАХ государствах вода...

Українська література, 6 лет назад

міні-твір "я патріот України"...

География, 6 лет назад

циркуляция атмосферы атмосферные фронты циклоны и антициклоны синоптические карты прогноз погоды...

Математика, 8 лет назад

Коля идёт к другу со скоростью 30 м/мин. Через сколько минут он к нему придёт, если расстояние до дома друга x м?

Математика, 8 лет назад

Срочно! Во сколько раз уменьшится объем прямоугольного параллепипеда если длину его уменьшить в 1,5 раза, высоту- в 2,2 раза, а ширину оставить без изменений.