Решите пожалуйста , очень надо

Ответы на вопрос
Ответ:
ниче не видно
Пошаговое объяснение:
Ответ:
1. 1) x∈(-∞; -1/2)∪(-1/2; +∞); 2) x∈[-4; 4]
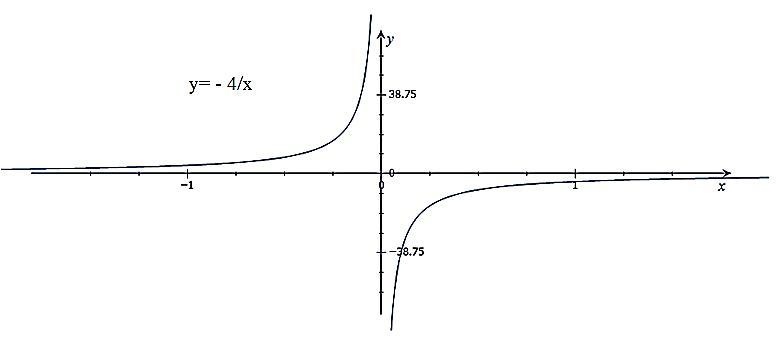
2. Рисунок приложен
1) y(-2)= 2 ; 2) x=-1/2 ; 3) x∈(-∞; 0)
4) x∈(-∞; 0) возрастает, x∈(0; +∞) убывает
3. Не проходит через точку M
Пошаговое объяснение:
1. Область определения функции
1) - функция дробная, поэтому знаменатель должен быть отличен от нуля: 2x+1≠0 или x ≠ -1/2. Тогда ООФ:
x∈(-∞; -1/2)∪(-1/2; +∞)
2) - эта функция определена, если подкоренное выражение не отрицательно:
16-x²≥0 или (4-x)(4+x)≥0. Применим метод интервалов
- + -
-∞ -----------[-4]-----[0]--------[4]------------ +∞
Тогда ООФ: x∈[-4; 4]
2. Рисунок приложен
1) y(-2)= -4/(-2)= 4/2=2
2) y=8 ⇒ -4/x= 8 ⇒ x= -4/8 = -1/2
3) y(x)>0 ⇔ -4/x>0 ⇔ 4/x < 0 ⇒ x<0 ⇔ x∈(-∞; 0)
4) Из рисунка определяем:
x∈(-∞; 0) возрастает, x∈(0; +∞) убывает
3. y(x)=x⁴-1, M(-2; -17)
y(-2)=(-2)⁴-1 = 16 -1 =15 ≠ -17, значит график функции не проходит через точку M.