Алгебра, вопрос задал liza1205006 , 6 лет назад

решите пожалуйста, много баллов​

Приложения:

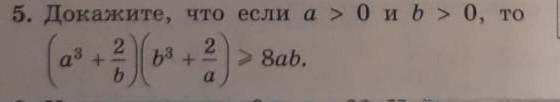
Ответы на вопрос

Ответил bb573878
2

Ответ:

Объяснение:

a>0;b>0

воспользуемся неравенством о средних

\bigg(a^3+\dfrac{2}{b} \bigg)\bigg(b^3+\dfrac{2}{a} \bigg)\geq 2\sqrt{a^3\cdot\dfrac{2}{b} }\cdot2\sqrt{b^3\cdot\dfrac{2}{a} } =4\sqrt{\dfrac{2a^3}{b}\cdot\dfrac{2b^3}{a} } =4\cdot2\sqrt{a^2b^2} =8ab

доказано

Предыдущий вопрос
Следующий вопрос
Новые вопросы
Қазақ тiлi, 1 год назад
помогите составить предложения - 1. қоңырау шаламын, 2. әдеп, 3. бола ма, 4. шақырып жіберіңізші, 5. телефон тұтқасы...
Українська мова, 1 год назад
однокореневі слова до слова підводний...
Биология, 6 лет назад
помогите!ЖПЖПЖПЖППЖПЖЖПЖПЖП...
Литература, 6 лет назад
что высмеивает Чехов в произведение Предложение????СРОЧНО!!!100 БАЛЛОВ​...
Математика, 8 лет назад
x^-x+9=(x+2)^ решить уравнение...
Алгебра, 8 лет назад
2-8 задание. В 5 просто сократить дробь. ПОМОГИТЕ ПРОШУ, САМОСТОЯТЕЛЬНАЯ СКОРО...