Алгебра, вопрос задал tema051203 , 1 год назад

Решите пожалуйста, как можно подробнее. Заранее спасибо!

Приложения:

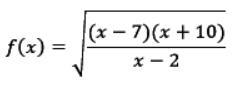
dontcallmeupp: А какое задание?

NNNLLL54: что надо сделать с функцией ?

tema051203: Надо найти область определения, но я не умею решать такие корни.

tema051203: Вроде должна получиться система, и её надо решить

NNNLLL54: для ООФ никакой системы не потребуется

Ответы на вопрос

Ответил NNNLLL54

$f(x)=\sqrt{\frac{(x-7)(x+10)}{x-2}}\\\\OOF:\; \; \; \frac{(x-7)(x+10)}{x-2}\geq 0\\\\znaki:\; \; \; ---[-10\, ]+++(2)---[\, 7\, ]+++\\\\\underline {x\in D(y)=[-10;2)\cup [\, 7;+\infty )}$

P.S Подкоренное выражение должно быть неотрицательным. Решаем неравенство методом интервалов.

tema051203: и никаких систем неравенств?

NNNLLL54: никаких... метод интервалов !

tema051203: спасибо огромное!!!

tema051203: А можно ещё попросить график функции по другой функции?

Ответил Аноним

Вы совершенно правы, именно система. И вот она.

(х-7)(х-2)(х+10)≥0

(х-2)≠0

неравенство решим, использовав метод интервалов. Приравняем нулю подкоренное выражение. найдем корни, выколем х=2, который обращает в нуль знаменатель, и определим знаки на образовавшихся интервалах. Нас интересуют знаки больше нуля или равно нулю. т.к. под корнем не может стоять число отрицательное.

____-10____2_______7___

- + - +

Область определения [-10;2)∪[7;+∞)

tema051203: помогите пожалуйста ещё с одним заданием оно у меня в вопросах

Аноним: уже

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Химия, 1 год назад

Допишіть рівняння реакцій: 1. K2CO3 +CaCl2→ 2. Cr(OH)3→ 3. FeSO3→ 4. SO3 +CaO→ 5. H2SO4+Mg(OH)2→ 6. AgNO3+K3PO4→ 7 CuSO4+NaOH → 8 Na2CO3+HCl→ Швидше будь ласка...

Алгебра, 1 год назад

‼️Допоможіть ‼️25б‼️‼️‼️‼️...