Решите пожалуйста эти задачи

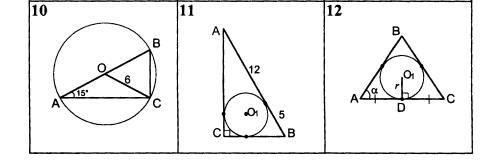
10) ОС – медиана, АВ – гипотенуза. АО = ОВ = 6.

Угол ВОС как центральный равен 15*2 = 30 градусов.

В треугольнике ОВС высота из точки В равна 6*sin 30 = 6*(1/2) = 3.

S(OBC) = (1/2)*6*3 = 9 кв. ед.

Медиана делит площадь треугольника пополам.

Ответ: S(ABC) = 9*2 = 18 кв. ед.

11) (12 + r)² + (5 + r)² = (12 + 5)².

144 + 24r + r² + 25 + 10r + r² = 289.

2r² + 34r – 120 = 0.

r² + 17r – 60 = 0.

Ищем дискриминант:

D=17^2-4*1*(-60)=289-4*(-60)=289-(-4*60)=289-(-240)=289+240=529;

Дискриминант больше 0, уравнение имеет 2 корня:

r_1=(2root529-17)/(2*1)=(23-17)/2=6/2=3;

r_2=(-2root529-17)/(2*1)=(-23-17)/2=-40/2=-20 (не принимаем).

Получаем катеты 5 + 3 = 8 и 12 + 3 = 15.

Ответ: S(ABC) = (1/2)*8*15= 60 кв. ед.

12) Угол С равен углу А.

Сторона АС = 2*(r/tg(α/2)) = 2r/tg(α/2)

Далее применим формулу: S = (a²/2)(sin α*sin β/sin γ).

Подставим в неё данные.

S = (4r²/tg²(α/2)/2)(sin² α/sin(180 - 2α) = (2r²/tg²(α)/2)(sin² α/sin(2α).

Ответ: S = (2r²/tg²(α)/2)(sin² α/sin(2α).