Алгебра, вопрос задал belkovan , 1 год назад

Решите пожалуйста эти системы , прошу Вас или одну любую
Это 2 разные системы
Пожалуйста

Приложения:

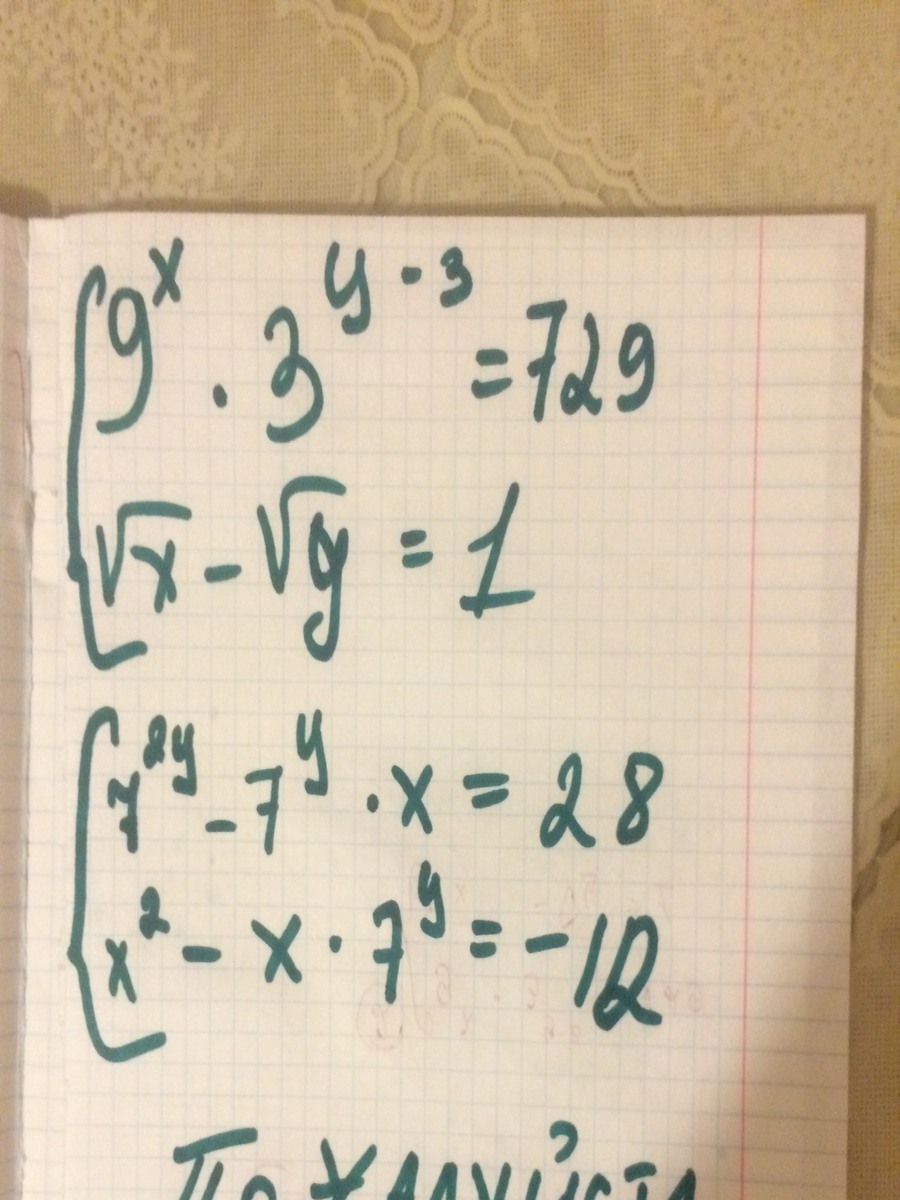
Ответы на вопрос

Ответил NNNLLL54

1

$\left \{ {{7^{2y}-7^{y}\cdot x=28} \atop {x^2-x\cdot 7^{y}=-12}} \right. \; \left \{ {{7^{y}(7^{y}-x)=28} \atop {x(x-7^{y})=-12}} \right. \left \{ {{7^{y}-x=\frac{28}{7^{y}} \atop {7^{y}-x=\frac{12}{x}}} \right. \\\\\frac{28}{7^{y}}=\frac{12}{x},\; x=\frac{7^{y}\cdot 12}{28}=\frac{7^{y}\cdot 3}{7}\\\\1)\; 7^{y}-7^{y}\cdot \frac{3}{7}=\frac{12}{x}\\\\7^{y}\cdot \frac{4}{7}=\frac{12}{x}\\\\7^{y}=\frac{21}{x}\\\\7^{y}\cdot x=21\\\\7^{2y}-21=28\\\\7^{2y}=49\; ,\; \; 7^{2y}=7^2\; ,\; \; 2y=2\; ,\; y=1$

$2)x^2-21=-12\\\\x^2=33\\\\x_1=\sqrt3 ,x_2=-\sqrt33\\\\otvet:(-\sqrt{33},1),(\sqrt{33},1)$

NNNLLL54: Извиняюсь, я пропустила во 2 пункте то, что справа -12. а не + 12.Тогда x^2-21=-12 , x^2=-12+21=9 , x=+-3. Ответ: (-3,1), (3,1).

belkovan: здравствуйте, помогите мне пожалуйста

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Английский язык, 1 год назад

Английский язык, помогите пожалуйста.

Русский язык, 1 год назад

1)Обязательно ли иметь много друзей ? 2)чем отличается друг от приятеля? Срооооочнооооо...

Биология, 1 год назад

митоз включает в себя ?

Физика, 1 год назад

1) на рисунке 1 дана схема цепи.Укажите направление тока. Покажите между какими точками должен быть включен вольтметр для измерения напряжения на лампах Л1 м Л2 2)Участок цепи состоит из трех...

Литература, 7 лет назад

Помогите пожалуйста сочинить сказку про не одушевлённый предмет! (любой) СРОЧНО...

Литература, 7 лет назад

5 Поговорок о волках...