Математика, вопрос задал Vladosikpapadosik , 1 год назад

Решите пожалуйста эти интегралы

Приложения:

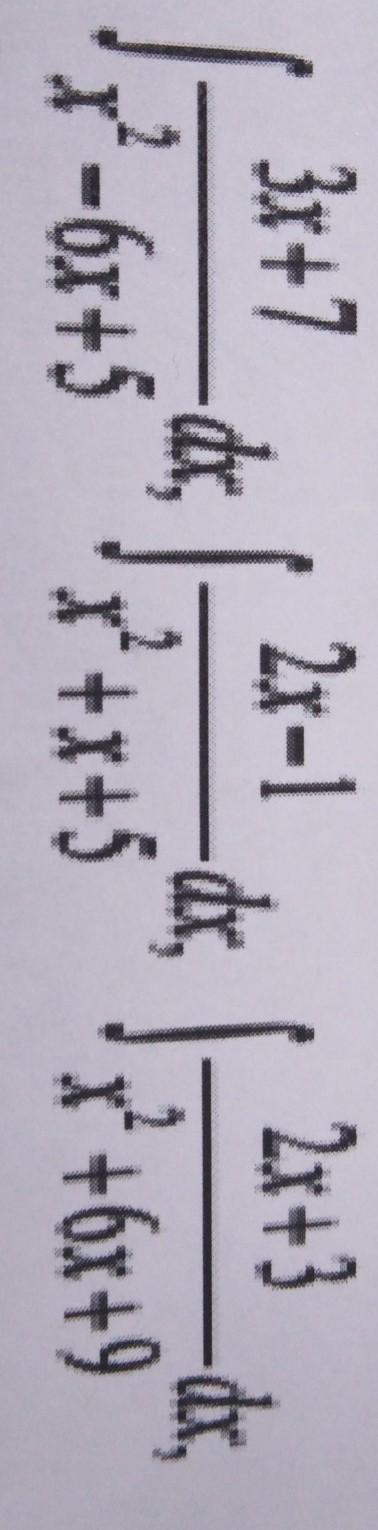
Ответы на вопрос

Ответил NNNLLL54

1

$1)\; \; \int \frac{3x+7}{x^2-6x+5}\, dx=\int \frac{3x+7}{(x-1)(x-5)}\, dx=\int \Big (\frac{-2,5}{x-1}+\frac{5,5}{x-5}\Big )\, dx=\\\\=-2,5\cdot ln|x-1|+5,5\cdot ln|x-5|+C$

$2)\; \; \int \frac{2x-1}{x^2+x+5}\, dx=\int \frac{2x-1}{(x+\frac{1}{2})^2+\frac{19}{4}}\, dx=[\; t=x+\frac{1}{2}\; ,\; x=t-\frac{1}{2}\; ]=\int \frac{2t-2}{t^2+\frac{19}{4}}\, dt=\\\\=\int \frac{2t\, dt}{t^2+\frac{19}{4}}\, dt-2\int \frac{dt}{t^2+\frac{19}{4}}\, dt=ln|t^2+\frac{19}{4}|-2\cdot \frac{2}{\sqrt{19}}\cdot arctg\frac{2t}{\sqrt{19}}+C=\\\\=ln|x^2+x+5|-\frac{4}{\sqrt{19}}\cdot arctg\frac{2x+1}{\sqrt{19}}+C$

$3)\; \; \int \frac{2x+3}{x^2+6x+9}\, dx=\int \frac{2x+3}{(x+3)^2}=[\; t=x+3\; ,\; x=t-3\; ,\; dx=dt\; ]=\\\\=\int \frac{2t-3}{t^2}\, dt=\int (\frac{2}{t}-\frac{3}{t^2})\, dt=2\cdot ln|t|+3\cdot \frac{1}{t}+C=2\cdot ln|x+3|+\frac{3}{x+3}+C$

Vladosikpapadosik: что со вторым?

NNNLLL54: перезагрузи страничку

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Химия, 1 год назад

ТЕРМІНОВО !!! Завдання 6 6. Складіть рівняння реакцій між речовинами:...

География, 1 год назад

повідомлення на тему "Забруднення вод Світового океану"...

Математика, 1 год назад

СРООООЧНО ДАЮ ;45 БААААААЛОВ Отрезок МР равен 7 см. Радиус окружности с центром в точке М равен 4 см. Радиус окружности с центром в точке Р равен 5 см. Чему равны длины отрезков MS и PT.

Литература, 1 год назад

Печорин начал говорить о княжне Мери Грушницкому с довольно приличного комплимента, а закончил цинично. Почему? Случайно ли Грушницкий уронил стакан? Что можно сказать о Мери в этом эпизоде?

Русский язык, 6 лет назад

112Б. Запиши на слух слова, которые характеризуют Казахстан. 1)казахи 2)бешпармак 3)баурсаки ...

Математика, 6 лет назад

Решите задачу. Полное решение задачи прикрепите к заданию. На выпускном в саду детям подарили одинаковые наборы. Во всех наборах вместе было 480 тетрадей в клетку, 448 тетрадей в линейку и 352...