Алгебра, вопрос задал vosipenokelizaveta , 6 лет назад

Решите пожалуйста))

Приложения:

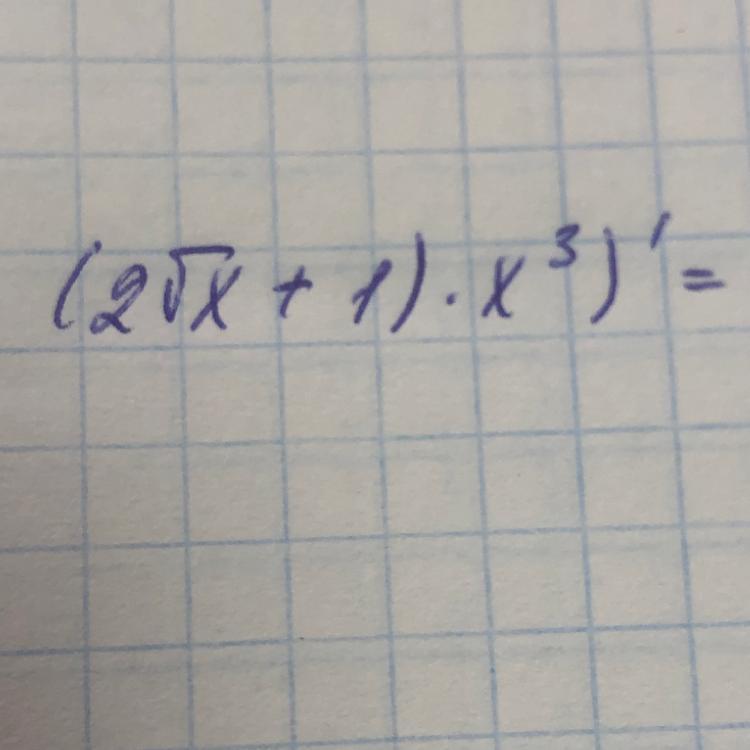
Ответы на вопрос

Ответил sergeevaolga5

Ответ:

$x^2(7\sqrt{x}+3)$

Объяснение:

$((2\sqrt{x}+1)*x^3)`=(2\sqrt{x}*x^3+x^3)`=(2x^{0,5}*x^3+x^3)`=\\\\=(2x^{3,5}+x^3)`=(2x^{3,5})`+(x^3)`=2*3,5x^{3,5-1}+3x^{3-1}=\\\\=7x^{2,5}+3x^2=7x^2*\sqrt{x}+3x^2=x^2(7\sqrt{x}+3)$

*******************************************************************

Для решения использованы формулы нахождения производных (табличные) и правило нахождения производной суммы двух функций:

$(x^n)`=n*x^{n-1}\\\\(f(x)+g(x))`=f`(x)+g`(x)$

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Русский язык, 1 год назад

что я знаю о блакаде много...

Английский язык, 1 год назад

Эссе на тему "having modern technologies at home is rather dangerous"...

Английский язык, 6 лет назад

Complete the sentences with the Present Simple passive form of the verbs in brackets.

Русский язык, 6 лет назад

И.п. трое лучших друзей Р.п. троих лучших друзей Д.п. троим лучшим друзьям В.п. троих лучших друзей Т.п. троими лучшими друзьями П.п. о троих лучших друзьях - Выделите окончания у числительных...

Химия, 8 лет назад

Помогите с химией 8 класс,как обьяснить выражение альфа равно 80% ?

Литература, 8 лет назад

Срочно помогите сдедать анализ стихотворения...