Алгебра, вопрос задал Vorobyshekkk , 2 года назад

Решите пожалуйста.....

Приложения:

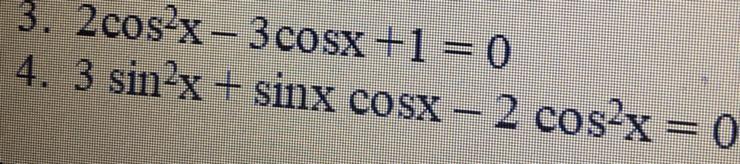
Ответы на вопрос

Ответил Miroslava227

Ответ:

Пусть cosx = t

$2 {t}^{2} - 3t + 1 = 0 \\ d = 9 - 8 = 1 \\ t1 = \frac{3 + 1}{4} = 1 \\ t2 = \frac{1}{2} \\ \\ \cos(x) = 1 \\ x1 = 2\pi \: n \\ \\ \cos(x) = \frac{1}{2} \\ x2 = + - \frac{\pi}{3} + 2 \pi \: n$

разделим на cos^2x, не равный 0

$3 {tg}^{2} x + tgx - 2 = 0 \\ \\ tgx = t \\ 3 {t}^{2} + t - 2 = 0 \\ d = 1 + 24 = 25 \\ t1 = \frac{ - 1 + 5}{6} = \frac{2}{3} \\ t2 = - 1 \\ \\ tgx = \frac{2}{3} \\ x1 = arctg( \frac{2}{3} ) + \pi \: n \\ \\ tgx = - 1 \\ x2 = - \frac{\pi}{4} + \pi \: n$

n принадлежит Z.

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Қазақ тiлi, 1 год назад

Помогите пж Познание мира Казак тiлi...

Русский язык, 1 год назад

По уши в ОГЭ и ЕГЭ! ОБРАЗОВАТЕЛЬНЫЙ БЛОГ КРЮКОВОЙ М.А. В ПОМОЩЬ УЧЕНИКУ И УЧИТЕЛЮ ПРИ ПОДГОТОВКЕ К ОГЭ И ЕГЭ ПО РУССКОМУ ЯЗЫКУ ▼ четверг, 27 ноября 2014 г. ОГЭ Н/НН в суффиксах разных частях...

Русский язык, 2 года назад

найди безличный глагол А.Разбедаться,Б.Не терпиться,В.вертелся...

Қазақ тiлi, 2 года назад

Тауелсиз казак когинде самгаймын мен кырандай Пж срочно ...

Математика, 7 лет назад

Прочитанных страниц в книге в 4 раза больше , чем непрочитанных. Сколько страниц может быть в книге: 142, 144, 145?Сколько прочитанных страниц в книге?

Обществознание, 7 лет назад

Средняя самооценка её сильные и слабые стороны Низкая самооценка её сильные и слабые стороны...