Алгебра, вопрос задал mentovsky1 , 1 год назад

Решите подробно, пожалуйста

Приложения:

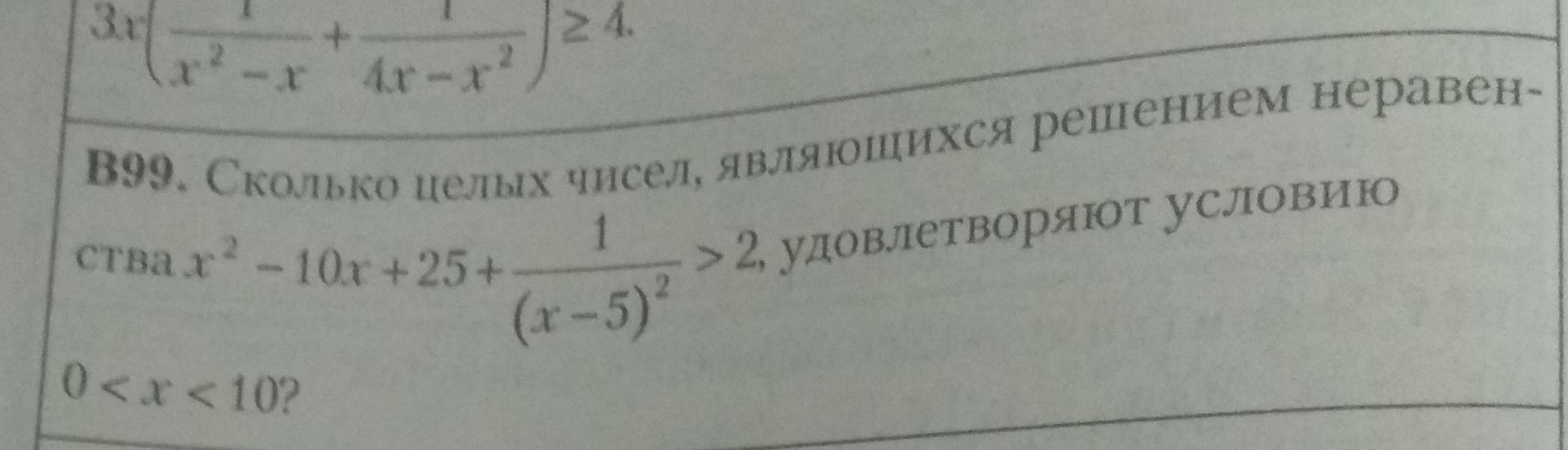
Ответы на вопрос

Ответил NNNLLL54

0

Ответ: 8 целых значений , являющихся решением заданного неравенства , удовлетворяют условию 0<x<10 .

Объяснение:

$(x^2-10x+25)+\frac{1}{(x-5)^2}>2\\\\(x-5)^2+\frac{1}{(x-5)^2}-2>0\; \; ,\; \; ODZ:\; (x-5)^2\ne 0\; \; \to \; \; x\ne 5\\\\t=(x-5)^2>0:\; \; \; t+\frac{1}{t}-2>0\; \; ,\; \; \frac{t^2-2t+1}{t}>0\; \; ,\; \; \frac{(t-1)^2}{t}>0\; ,\\\\znaki:\; \; \; ---(0)+++[\, 1\, ]+++\; \; \; \; t\in (0,1\, ]\cup [1,+\infty )\; \; \to \\\\t\in (0,+\infty )\; \; \Rightarrow \; \; (x-5)^2>0\; \; \Rightarrow \; \; x-5\ne 0\; \; ,\; \; x\ne 5\; \; \Rightarrow \\\\x\in (-\infty ,5)\cup (5,+\infty )$

$0<x<10:\; \; x=1\; ,\; 2\; ,\; 3\; ,\; 4\; ,\; 6\; ,\; 7\; ,\; 8\; ,\; 9\; \; (x\ne 5)\\\\Otvet:\; \; 8\; \; celux\; znachenij\; .$

LFP: х≠6, т.к. t≠1...

NNNLLL54: да, упустила...

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Қазақ тiлi, 1 год назад

Менің мамандығым тақырыбына диалог жазу...

Геометрия, 1 год назад

Квадратный лист бумаги разделён на 6 прямоугольников. Сумма периметров всех шести прямоугольников равна 120. Чему равна площадь листа бумаги?

Русский язык, 1 год назад

Допустима ли форма слова "водросль" (водросли), вместо водОросль?

Математика, 1 год назад

Поможіть розв'язати математика 6 клас...

Математика, 6 лет назад

СРОЧНО! 15 БАЛЛОВ Решите уравнение Система неравенств 3х - 1 < 0 x^2 - 3x + 2 >= 0...

География, 6 лет назад

. На каких горных вершинах температура воздуха равна 0°С (с каждым километром температура понижается на 6°): А. Температура воздуха у подножия +26°, высота горы – 3 км Б. Температура воздуха у...