Алгебра, вопрос задал hiddenmaier , 6 лет назад

решите определённый интеграл

Приложения:

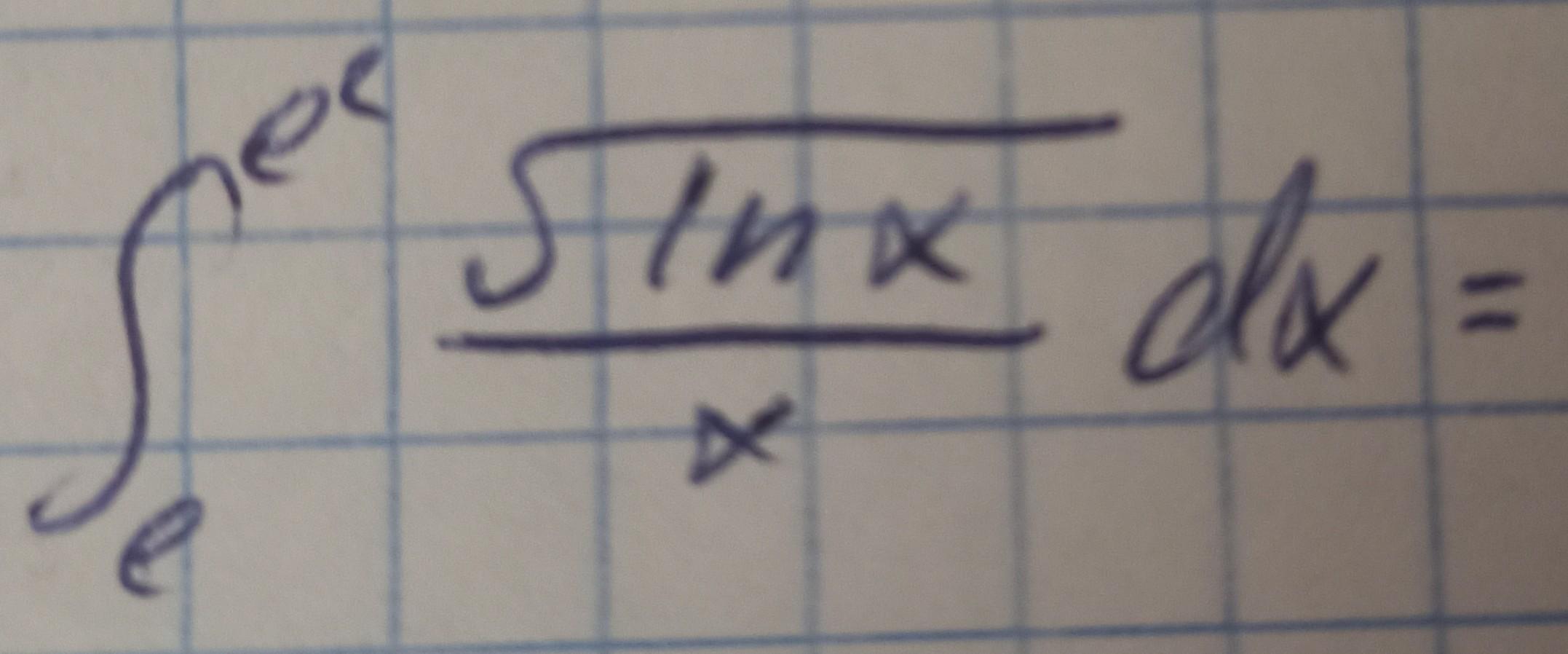
Ответы на вопрос

Ответил kamilmatematik100504

Ответ:

$\cfrac{4\sqrt{2} -2 }{3}$

Объяснение:

Множество первообразных можно найти с помощью неопределенного интеграла, воспользовавшись формулами :

$\sf \displaystyle \int\limits x^n \, dx = \frac{x^{n+1} }{n+1} +C~, ~ n \neq -1 \\\\\\ \int\limits f(x)\cdot g'(x) \, dx = \int\limits f(x) d(g(x))\, dx \\\\\\ d (f(x) ) = d(f(x)+C)$

Формула Ньютона - Лейбница

$\sf \displaystyle f(x) = F'(x)\\\\ \int\limits^a_b {f(x)} \, dx = F(x) \bigg | ^a _ b = F(a) - F (b )$

Сделаем замену

$\ln x = t\\\\\sqrt{\ln x} =\sqrt{t} \\\\ \dfrac{1}{x} dx = d t$

$\displaystyle \int\limits^{} {\frac{\sqrt{\ln x } }{x} } \, dx = \int\limits^{} {} \sqrt{t} \, dt = \frac{t^{\tfrac{1}{2}+ 1 }}{\dfrac{1}{2}+ 1 } = \frac{2t^{\tfrac{3}{2} }}{3} + C$

Подставим $\ln x = t$ и вычислим определенный интеграл c помощью формулы Ньютона - Лейбница

$\displaystyle \int\limits^{e^2}_e {\frac{\sqrt{\ln x } }{x} } \, dx =\frac{2 (\ln x) ^{\tfrac{3}{2} }}{3} ~ \Bigg | ^{e^2} _ {e} = \frac{2(\ln e^2)^{\tfrac{3}{2} }}{3} } - \frac{2(\ln e)^{\tfrac{3}{2} }}{3} } = \frac{4\sqrt{2} -2 }{3}$