Решите неравенство подробно
Ответ: (-бескон ; 2] ;[3 ;+бескон)
Приложения:
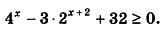
Ответы на вопрос
Ответил hlopushinairina
2
4^x-3·2^(x+2)+32≥0;⇒
4^x=2^(2x);2^(x+2)=2²·2^x=4·2^x;⇒
2^(2x)-12·2^x+32≥0;⇒
2^x=y;y>0;⇒
y²-12y+32≥0;
y₁,₂=6⁺₋√36-32=6⁺₋√4=6⁺₋2;
y₁=8;y₂=4;⇒
y≤4;y≥8;
2^x≤4;⇒x≤2;⇒(-∞;2];
2^x≥8;⇒x≥3;⇒[3;+∞)
4^x=2^(2x);2^(x+2)=2²·2^x=4·2^x;⇒
2^(2x)-12·2^x+32≥0;⇒
2^x=y;y>0;⇒
y²-12y+32≥0;
y₁,₂=6⁺₋√36-32=6⁺₋√4=6⁺₋2;
y₁=8;y₂=4;⇒
y≤4;y≥8;
2^x≤4;⇒x≤2;⇒(-∞;2];
2^x≥8;⇒x≥3;⇒[3;+∞)
Ответил julyap
1
+ - +
--------------|--------------|----------------------> x
2 3
Новые вопросы