Математика, вопрос задал DexterWizero , 7 лет назад

Решите неравенство: log7 x+log7(x-1)>log7 2

Ответы на вопрос

Ответил MaxikMK

0

Решить неравенство.

Сразу же введём ОДЗ, чтобы потом о нём не забыть. Подлогарифмическое выражение должно быть строго положительным. Выберем наименьшее из них. Получим, что $x - 1 > 0 Rightarrow x > 1.$

$log_7x + log_7(x - 1) > log_72;\log_7x + log_7(x - 1) > log_72;\log_7x(x-1) > log_72.$

Так как основание логарифма больше единицы [7 > 1], то от него можно избавиться без смены знака неравенства.

$x(x - 1) > 2;\x^2 - x - 2 > 0;\D = left[b^2 - 4acright] = 1 - 4 cdot 1cdot (-2) = 1 + 8 = 9 = 3^2;\x_{1,2} = left[dfrac{-bpmsqrt{D}}{2a}right] = dfrac{1pm3}{2} = left[begin{array}{c}-1,&2.end{array}$

$(x + 1)(x - 2) > 0;\x in (-infty; -1); U; (2; +infty).$

Но, учитывая ОДЗ, записанное в начале: $x in (2; +infty).$

Ответ: $x in (2; +infty).$

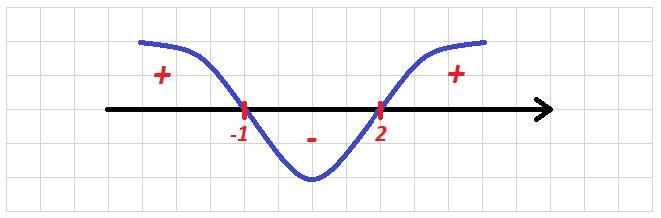
Приложения:

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Английский язык, 1 год назад

HELP Пожалуйста помогите с диалогом по английскому (11 класс) 65+ баллов (задание внутри) ...

Русский язык, 1 год назад

это час слаженной кипучей работ... (какая буква здесь будет)...

Математика, 7 лет назад

ПОМОГИТЕ СРОЧНО ПОЖАЛУЙСТА Радиусы основания усеченного конуса равны 12 и 6 см, а образующая наклона к плоскости основания под углом 45°. Найдите площадь и обьем усеченного конуса...

Математика, 7 лет назад

как это решить помогите пожалуйста ...

Математика, 8 лет назад

Напишите формулу квадратного уравнения и как она звучит. Срочно!

Математика, 8 лет назад

отрезок AB длина которого равна половине длины отрезка в 1 дм...