Решите неравенство, которое на фото. Срочно!
Приложения:
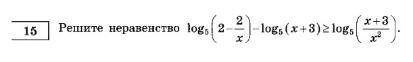
Ответы на вопрос
Ответил pushpull
0
Ответ:
Пошаговое объяснение:
первым делом области определения для логарифмов
(2-2/х) > 0 ⇒ x > 1
x+3 > 0 ⇒ x > -3
x(2x-2) ≥ (x+3)²
x² -8x -9 ≥ 0
x² -8x -9 = 0 ⇒ x1=-1 x2= -9
парабола ветвями вверх, поэтому неравенство выполняется для
х ∈(-∞; -1) ∩ (9; 0)
теперь учтем области определения логарифмов и получим
ответ
х ∈ (-3; -1) ∩ (9; +∞)
Новые вопросы