Алгебра, вопрос задал eugeniodepez , 6 лет назад

Решите неравенства:

помогите пожалуйста

Приложения:

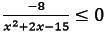
Аноним: я первый

Ответы на вопрос

Ответил Universalka

$\displaystyle\bf\\\frac{-8}{x^{2} +2x-15} \leq 0\\\\\\\frac{8}{x^{2} +2x-15} \geq 0\\\\\\x^{2} +2x-15 > 0\\\\\\(x+5)(x-3) > 0$

+ + + + + (- 5) - - - - - (3) + + + + +

//////////// /////////////

$\displaystyle\bf\\Otvet: \ x\in\bigg(-\infty \ ; \ -5\bigg) \ \cup \ \bigg(3 \ ; \ +\infty\bigg)$

Ответил Vopoxov

Объяснение:

$\frac{ - 8}{ {x}^{2} + 2x - 15 } \leqslant 0 \: \: < = > \: \: \frac{ 8}{ {x}^{2} + 2x - 15 } \geqslant 0$

Рассмотрим выражение в знаменателе дроби и найдем значения х, в которых знаменатель обращается в нуль.

Для этого разложим на множители квадратный многочлен знаменателя:

${ {x}^{2} + 2x - 15 } = 0$

По Т Виета:

$\begin{cases} x_1+x_2 = -2\\ x_1\cdot x_2 = -15\end {cases} \qquad \begin{cases} - 5 + 3 = -2\\ - 5 \cdot 3= -15\end {cases}$

Отсюда:

$x_1= -5;\;\, x_2=3 \: \: = > \\ = > \: \: {x}^{2} + 2x - 15 =(x + 5) (x - 3)$

$\small \frac{ 8}{ {x}^{2} + 2x - 15 } \geqslant 0 \: \: < = > \: \: \frac{8}{(x + 5)(x - 3)} \geqslant 0 \\$

Рассмотрим числовую прямую. Найденные точки обозначаем "выколотыми", т к. в них знаменатель обращается в ноль, и они не входят в область определения.

см. на рис.

Получаем ответ:

Приложения:

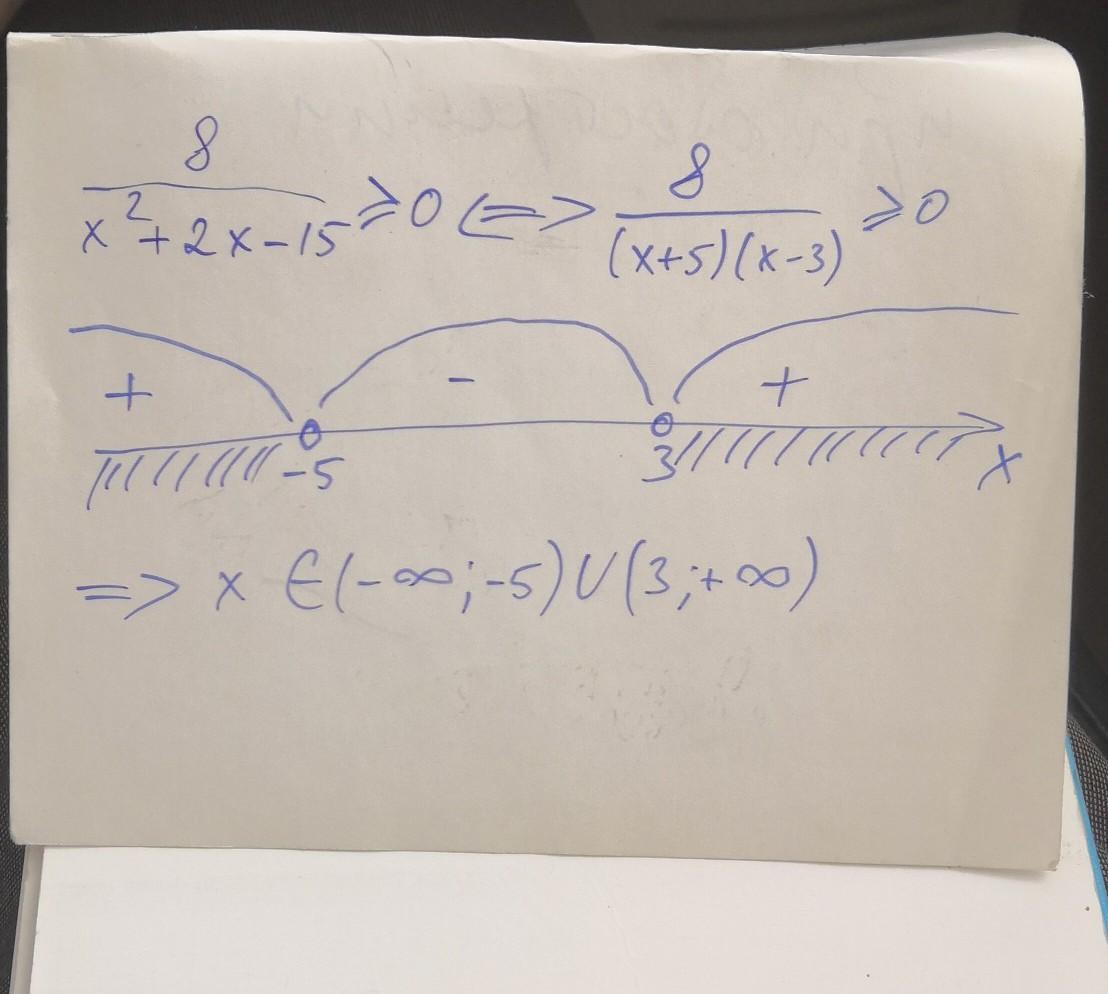
Новые вопросы

Русский язык, 1 год назад

Русский язык, 1 год назад

Математика, 6 лет назад

Геометрия, 6 лет назад

Математика, 8 лет назад

Математика, 8 лет назад