Решите логарифмическое неравенство
Приложения:
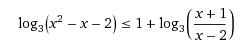
Ответы на вопрос
Ответил marat72
0
ОДЗ:
(x+1)/(x-2)>0

x^2-x-2=0
D=1+4*2=9=3²
x1=(1+3)/2=2
x2=(1-3)/2=-1
+ - +
--------¤-----------¤------------------->
-1 2
x∈(-∞;-1) u (2;+∞)
РЕШЕНИЕ:
log3 (x²-x-2)-log3 (x+1)/(x-2)≤1
x²-x-2 можно расписать как (x+1)*(x-2)
разность логорифмов с одинаковым основанием равно логорифму частного
log3 (x+1)*(x-2)*(x-2)/(x+1)≤1
log3 (x-2)²≤1
log3 (x-2)²≤log3 (3)
(x-2)²≤3
x²-4x+4≤3
переносим все в левую часть
x²-4x+1≤0
решаем методом интервалов
x²-4x+1=0
D1=4-1=√3
x1=2+√3
x2=2-√3
///////// + - //-//////////+/////////
---------¤-------•--------¤---------•------⇒
-1 2-√3 2 2+√3
c учетом ОДЗ x∈(2;2+√3]
Ответ:(2;2+√3]
вроде так, но я не уверен
(x+1)/(x-2)>0
x^2-x-2=0
D=1+4*2=9=3²
x1=(1+3)/2=2
x2=(1-3)/2=-1
+ - +
--------¤-----------¤------------------->
-1 2
x∈(-∞;-1) u (2;+∞)
РЕШЕНИЕ:
log3 (x²-x-2)-log3 (x+1)/(x-2)≤1
x²-x-2 можно расписать как (x+1)*(x-2)
разность логорифмов с одинаковым основанием равно логорифму частного
log3 (x+1)*(x-2)*(x-2)/(x+1)≤1
log3 (x-2)²≤1
log3 (x-2)²≤log3 (3)
(x-2)²≤3
x²-4x+4≤3
переносим все в левую часть
x²-4x+1≤0
решаем методом интервалов
x²-4x+1=0
D1=4-1=√3
x1=2+√3
x2=2-√3
///////// + - //-//////////+/////////
---------¤-------•--------¤---------•------⇒
-1 2-√3 2 2+√3
c учетом ОДЗ x∈(2;2+√3]
Ответ:(2;2+√3]
вроде так, но я не уверен
Новые вопросы
Русский язык,
1 год назад
Русский язык,
1 год назад
Математика,
1 год назад
Математика,
7 лет назад
История,
7 лет назад