решите иррациональное уравнение
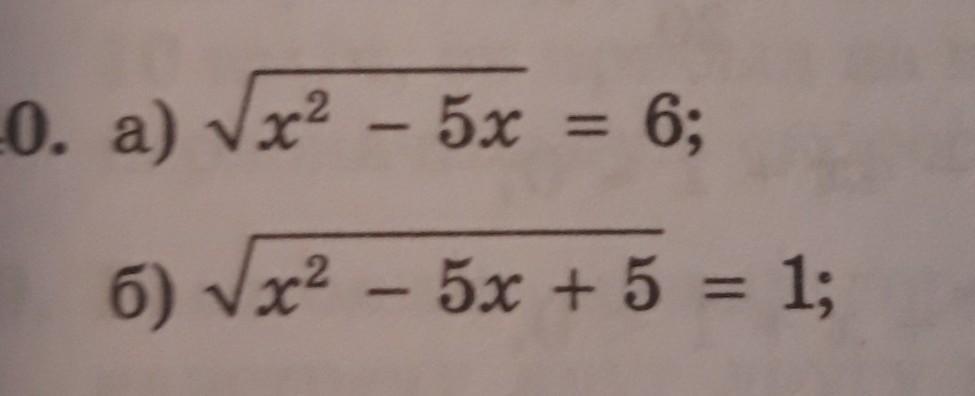
Ответы на вопрос
Ответ: а) х1=9, х2=-4, б) x1=4, x2=1.
Объяснение:
а) так как выражение x²-5*x находится под знаком корня, то прежде всего должно выполняться условие x²-5*x≥0. Решая это неравенство, находим, что x∈(-∞;0]∪[5;∞). Возводя обе части в квадрат и перенося 36 в левую часть, приходим к квадратному уравнению x²-5*x-36=0. Его дискриминант D=(-5)²-4*1*(-36)=169=13², откуда x1=(5+13)/2=9 и x2=(5-13)/2=-4. Так как оба эти корня удовлетворяют неравенству x²-5*x≥0, то оба они являются и решением заданного уравнения.
б) так как выражение x²-5*x+5 находится под знаком корня, то прежде всего должно выполняться условие x²-5*x+5≥0. Решая это неравенство, находим, что x∈(-∞;(5-√5)/2]∪[(5+√5)/2;∞). Возводя обе части в квадрат и перенося 1 в левую часть, приходим к квадратному уравнению x²-5*x+4=0. Его дискриминант D=(-5)²-4*1*4=9=3², откуда x1=(5+3)/2=4 и x2=(5-3)/2=1. Так как оба эти корня удовлетворяют неравенству x²-5*x+5≥0, то оба они являются и решением заданного уравнения.