Решите четвёртую систему уравнений
Приложения:
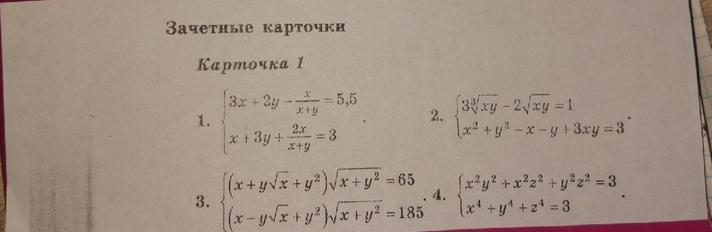
Ответы на вопрос
Ответил mathgenius
0
Ответ:
(1;1;1) ;(-1;1;1) ;(1;-1;1) ;(1;1;-1) ;(1;-1;-1) ;(-1;1;-1); (-1;-1;1) ;(-1;-1;-1)
Пошаговое объяснение:
Умножим обе части второго уравнения на 2,получаем:
2*x^4+2*y^4+2*z^4=6
перепишем его следующим образом:
(x^4+y^4) +(x^4+z^4) +(y^4+z^4)=6
аналогично умножим первое уравнение на -2 и получим:
-2*x^2*y^4 -2*x^2*z^2 -2*y^2*z^2=-6
Cложив попарно имеем:
(x^2-y^2)^2 +(x^2-z^2)^2 +(y^2-z^2)^2=0
Cумма квадратов 0,только когда каждый из них 0.
Очевидно что это происходит когда:
x^2=y^2=z^2
x^4=y^4=z^4=3/3=1
Значит решения это все комбинации 1 и -1.
(1;1;1) ;(-1;1;1) ;(1;-1;1) ;(1;1;-1) ;(1;-1;-1) ;(-1;1;-1); (-1;-1;1) ;(-1;-1;-1)
Новые вопросы
Русский язык,
1 год назад
Геометрия,
7 лет назад
Геометрия,
7 лет назад
Литература,
8 лет назад
Литература,
8 лет назад