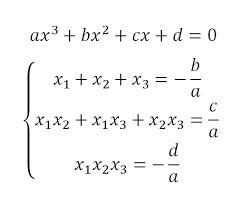решите !!!!!!!!!!!!!!!!!!!
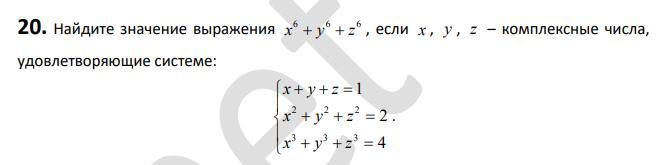
Ответы на вопрос
Ответ:
Объяснение: у кубического уравнения у которого корни x;y;z есть свойства (смотрите на фото)
найдем
чтобы найти
будем использовать формулу
=>
=> получим уравнение
корни которого
=>
используем уравнение которое мы вывели снова тогда выйдет =>
упростим
теперь наше уравнение будет иметь каноничный вид
теперь подставим значения и выйдет