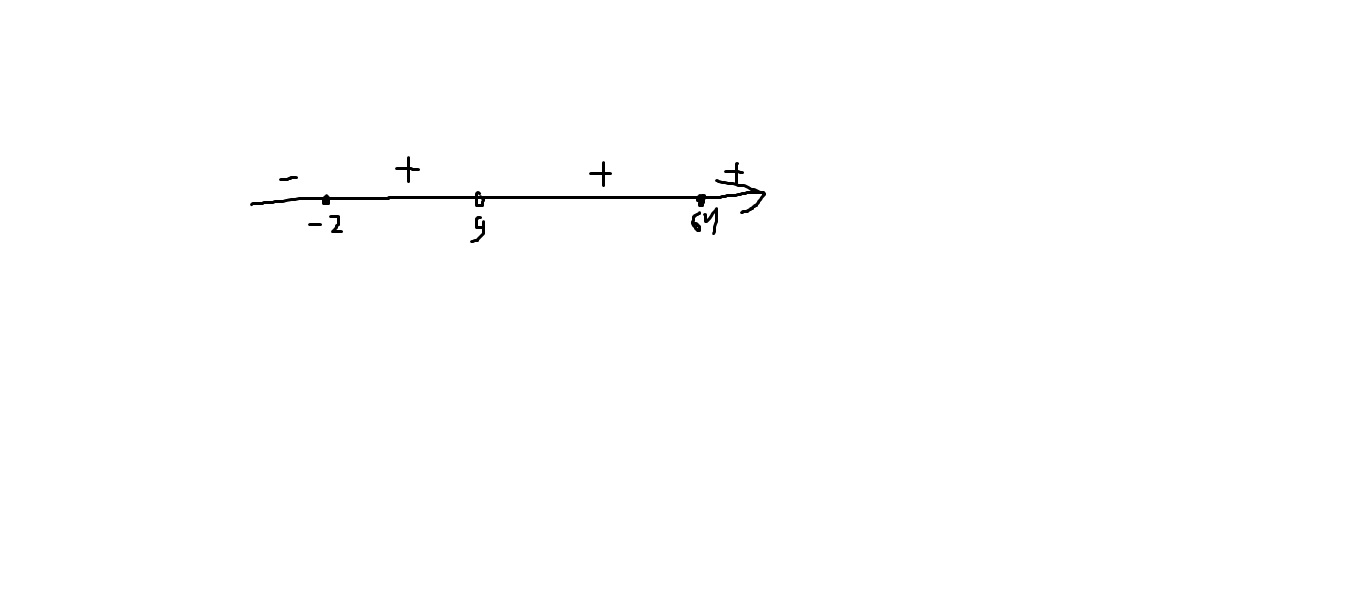Решить задания, обведенные кружочком, если есть время, то еще и 10,11,12. Смотрите во вложения :) Чтобы проверить правильность решенного на второй картинке есть ответы. Мне нужно полное решение заданий, обведенных кружочком.


Ответы на вопрос
5. в) Здесь всё уже разбито на множители, поэтому осталось только нанести нули и не имеющие смысла выражения на прямую и верно поставить знаки. рисунок первого решения сейчас приложу. Отсюда выписываем те интервалы, где значение выражения меньше или равны 0. Это (-∞;-2] ∨ {64}
6.a) У нас выражение - дробь. А дробь имеет смысл, если его знаменатель не равен 0. С другой стороны - в знаменателе у нас стоит квадратный корень, который имеет смысл, если его подкоренное выражение неотрицательно. Отсюда естественно вытекает, что подкоренное выражение должно быть только больше нуля. составим и решим неравенство:
(4 - x)(x + 6) >0
Вынесем минус за скобки в левой части и домножим всё на -1:
-(x - 4)(x + 6) > 0
(x - 4)(x + 6) <0
Теперь в действие вступает стандартный метод интервалов. Получаем в результате интервал:
(-6;4)
Это и будет областью определения функции.
7)Чтобы решить систему неравенств, необходимо сначала решить по-отдельности каждое неравенство, а затем найти объединение полученных промежутков. Решим первое неравенство:
x² - x - 2 > 0
(x - 2)(x + 1) > 0
Решая методом интервалов, получим:
(-∞;-1) ∨ (2;+∞)
Решаем второе неравенство:
10x + 25 > 0
10x > -25
x > -2.5
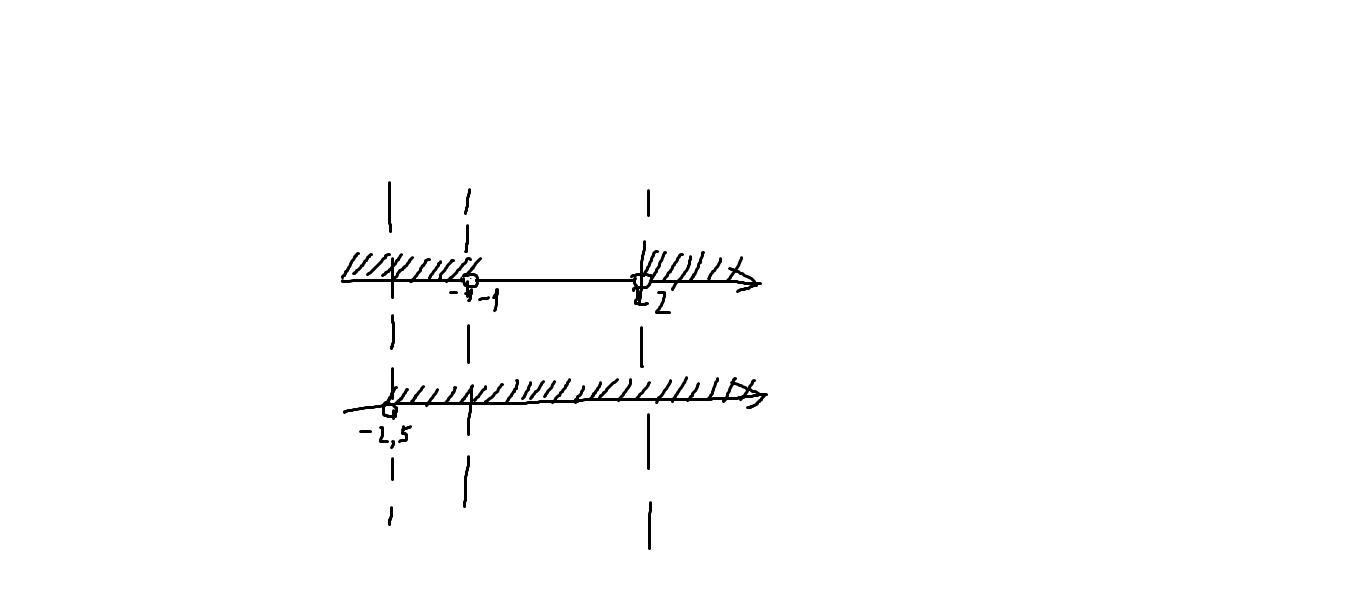
Теперь приведу рисунок, на котором найду окончательное решение всей системы. на рисунке решения каждого неравенства показаны штриховкой, решением системы соответственно будут участки, где штриховки совпадают, я их и нашёл. Это:
(-2.5;-1) ∨ (2;+∞) - решение системы.
10)а) Следует помнить, что решение неравенств высших порядков(степени, выше первой) должно осуществляться с помощью метода интервалов. Для этого, условие номер 1 - разложить исходное выражение на множители. Этим и займёмся. Разложим на множители левую часть неравенства:
16x³ - 32x² - x + 2 = (16x³ - 32x²) - (x - 2) = 16x²(x - 2) - (x-2) = (x-2)(16x² - 1) = (x-2)(4x-1)(4x+1)
Неравенство примет вид:
(x-2)(4x - 1)(4x+1) <0
Теперь решаем обычным методом интервалов, посколько коэффициенты при x уже положительны. Решая, получаем следующий промежуток:
(-∞;-1/4) ∨ (1/4;2) - это решение данного неравенства.