Решить задачу, на фотографии.
Подробно.
Приложения:

IUV:
ответ для сравнения существует ?
у меня получается в корень(7) раз
В 2 раза.
значит буду искать ошибку (
ошибку нашел, исправил, был знак минус в этой строке 4*3/2*p1*V1=3*p1V1*(k^2-1)/2 + p1V1*(k^2-1)/2
было так 4*3/2*p1*V1=3*p1V1*(k^2-1)/2 - p1V1*(k^2-1)/2
надо так 4*3/2*p1*V1=3*p1V1*(k^2-1)/2 + p1V1*(k^2-1)/2
+.
Ответы на вопрос
Ответил IUV
2
p=p1*V/V1 - зависимость давления от объема прямо пропорциональна
A=integral [1;2] pdV =p1/V1 * integral [1;2] VdV= p1/V1* V^2/2 [1;2] = p1/V1*(V2^2-V1^2)/2 = p1*V1*((V2/V1)^2-1)/2
пусть V2/V1 = к
A=p1/V1*(V2^2-V1^2)/2 =p1V1*(k^2-1)/2
****************то же самое без интегралов (см рисунок)*******************************
работа = площадь фигуры в координатах pV
работа = площадь трапеции = высота * средняя линияработа = (V2-V1)*(p1+p2)/2 V2/V1=p2/p1=k => работа = V1*(k-1)*p1*(k+1)/2=p1*V1*(k^2-1)/2 *********************************************************************************
U1=3/2*R*T1=3/2*p1*V1
U2=3/2*R*T2=3/2*p2*V2=k^2*3/2*p1*V1
U2-U1=3/2*R*(T2-T1)=3*p1V1*(k^2-1)/2
Q=U2-U1+A
4*U1=U2-U1+A
4*3/2*p1*V1=3*p1V1*(k^2-1)/2 + p1V1*(k^2-1)/2
4*3=3*(k^2-1) + (k^2-1)
3=(k^2-1)
k^2=4
k=2
A=integral [1;2] pdV =p1/V1 * integral [1;2] VdV= p1/V1* V^2/2 [1;2] = p1/V1*(V2^2-V1^2)/2 = p1*V1*((V2/V1)^2-1)/2
пусть V2/V1 = к
A=p1/V1*(V2^2-V1^2)/2 =p1V1*(k^2-1)/2
****************то же самое без интегралов (см рисунок)*******************************
работа = площадь фигуры в координатах pV
работа = площадь трапеции = высота * средняя линияработа = (V2-V1)*(p1+p2)/2 V2/V1=p2/p1=k => работа = V1*(k-1)*p1*(k+1)/2=p1*V1*(k^2-1)/2 *********************************************************************************
U1=3/2*R*T1=3/2*p1*V1
U2=3/2*R*T2=3/2*p2*V2=k^2*3/2*p1*V1
U2-U1=3/2*R*(T2-T1)=3*p1V1*(k^2-1)/2
Q=U2-U1+A
4*U1=U2-U1+A
4*3/2*p1*V1=3*p1V1*(k^2-1)/2 + p1V1*(k^2-1)/2
4*3=3*(k^2-1) + (k^2-1)
3=(k^2-1)
k^2=4
k=2
Приложения:
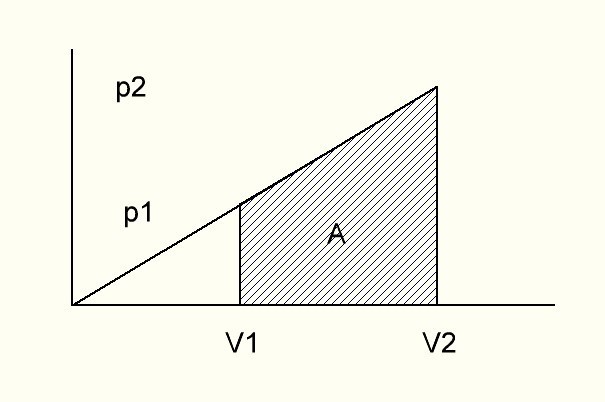
А есть решение без интегралов? Не изучал еще.
работа = площадь фигуры в координатах pV
работа = (V2-V1)*(p1+p2)/2
V2/V1=p2/p1=k => работа = V1*(k-1)*p1*(k+1)/2=p1*V1*(k^2-1)/2
Когда пишем энергию, моли не нужны в формуле?
не нужны
Новые вопросы
Геометрия,
1 год назад
Математика,
1 год назад
Физика,
1 год назад
Литература,
1 год назад
Алгебра,
7 лет назад