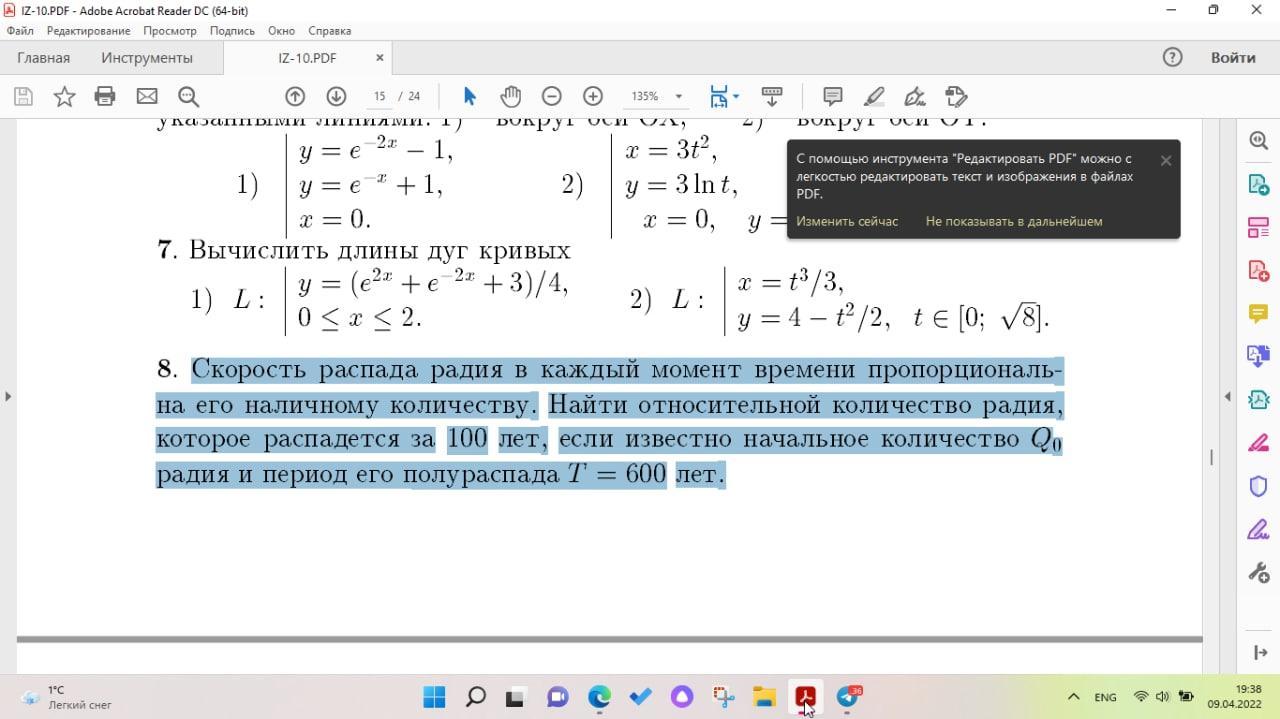
Математика, вопрос задал kolxic , 6 лет назад

Решить выделенную задачу, составив интеграл.

Приложения:

Ответы на вопрос

Ответил mathkot

Ответ:

За сто лет распадется приблизительно $0,9Q_{0}$ радия

Пошаговое объяснение:

По условию известно, что период полураспада радия 600 лет, то есть $T = 600$ это означает, что за 600 лет от массы радия останется только половина, а через еще 600 лет половина половины и так далее.

По условию известно, что скорость распада радия в каждый момент времени пропорциональна его имеющемуся количеству.

Составим функцию $y(t)$ котора будет описвать какое количество радия распадется в данный момент времени $t.$ Пусть $m$ это количество радия в текущий момент времени, $k$ - коэффициент пропорциональности.

То есть $y(t) = mkt$ , таким образом $y(t)$ показывает какая масса радия распалась в момент $t$ . Однако масса тоже меняется от времени. Поэтому данная формула не описывает изменние массы, а она

также меняется по закону $y(t) = mkt$ .

Модифицируем функцию, чтобы она учитывала изменение массы.

Рассмотрим значение массы в предыдущий момент.

В предыдуший момент масса была $y(t - зt)$ при $зt \to 0$ .

То есть таким образом за время $зt \to 0$ масса изменилась на:

$y(t) - y(t - зt) = mkt - mk(t - зt) = mkt - mkt + mkзt = mkзt$

Пусть $зm = y(t) - y(t - зt)$ , то есть насколько изменилась масса.

Тогда получилось, что за время $зt \to 0$ масса меняется по закону:

$зm = mkзt$

Перепишем данное выражение:

$зm = mkзt |: зt$

$\dfrac{зm}{зt} = mk$ , а так как $зt \to 0$ , то по определению предела можем написать следующие:

$\lim_{зt \to 0} \dfrac{зm}{зt} = mk$ .

Так как по определению производной $y'(t) = \lim_{зt \to 0} \dfrac{зm}{зt}$ , то сразу перепишем производную $y(t)$ через дифференциалы в виде:

$y'(t) = \dfrac{dm}{dt}$ . Таким образом подставив соотношение производную получим:

$\dfrac{dm}{dt} = mk \bigg |\cdot \dfrac{dt}{m}$ - решаем дифференциальное уравнение методом разделения переменных

$\dfrac{dm}{m} = k \cdot dt$ - проинтегриуем

$\displaystyle \int \dfrac{dm}{m} = \int k \cdot dt$

$\displaystyle \int \dfrac{dm}{m} = k \int 1 \cdot dt$

$\ln m + C_{1} = kt + C_{2}$

$\ln m = kt + C_{2} - C_{1}$

$\ln m = kt + \ln C$

$\ln m - \ln C = kt$

$\ln \bigg( \dfrac{m}{C} \bigg) = kt$

$m = Ce^{kt}$ - общее решение ( $m$ - функция зависящая от $t$ ).

Однако при составлении данного уравнения мы предположили, что в предыдущий момент времени у нас была какая-то масса, а по условию начальная масса $Q_{0}$ , что возможно учесть в уравнении как константу $C$ .

Тогда зададим начальные условия:

В начальный момент времени $t = 0$ и масса $m = Q_{0}$

$Q_{0} = Ce^{k \cdot 0}$

$Q_{0} = Ce^{0}$

$Q_{0} = C \cdot 1$

$Q_{0} = C$ , таким образом $m = Q_{0}e^{kt}$ , а из условия известно, то за время полупериода распадется половина массы, то есть $m = \dfrac{Q_{0}}{2}$ за $T$ .