Решить в целых числах с очень подробным объяснением...
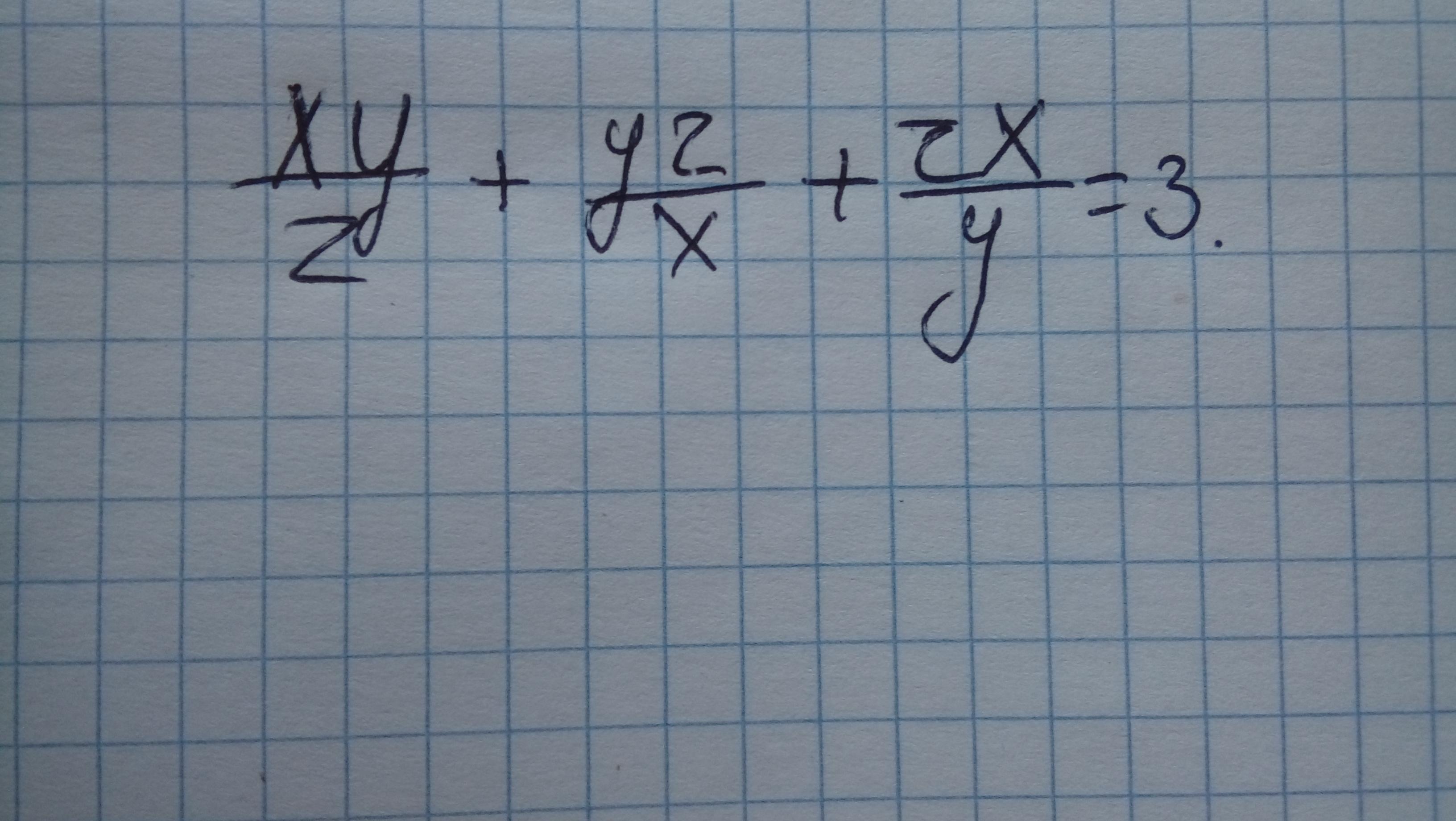
Ответы на вопрос
Объяснение:
Рассмотрим числа x y z:
1) Если все положительные x y z, то и результат будет положительный.
2) Если одно из значений отрицательно, то каждая дробь будет отрицательной и ответ будет отрицательный:
К примеру возьмём x=10, y=10, z=-10
3)Если два отрицательных, то ответ будет положительным (аналогично 2 примеру)
4)и наконец 3 отрицательных, все дроби отрицательные⇒ответ отрицательный.
Т.к. наше выражение =3>0, то нас устраивают случаи 1) и 3).
Преобразуем равенство, умножив на 2xyz(x,y,z≠0):
5) Отсюда видно что если числа x, y, z являются решением, то, изменив знак у любых двух чисел из этой тройки, мы снова получим решение уравнения. Поэтому достаточно рассмотреть положительные решения, а оставшиеся получить путем чередования двух минусов.
Рассмотрим левую часть уравнения:
Помним, что квадрат числа неотрицательное число, поэтому:
Значит наше выражение:
Вспомним что изначальное выражение равнялось 6xyz:
Т.к. x,y,z положительные, то в натуральных числах есть одно решение: (1,1,1).
Учитывая 5 пункт получаем 4 решения:
(1,1,1), (-1;-1;1), (-1;1;-1), (1;-1;-1)