Решить уравнение

Ответ: x=п/4+пn/2
x=+- 
Номер 69 под цифрой один.
Приложения:
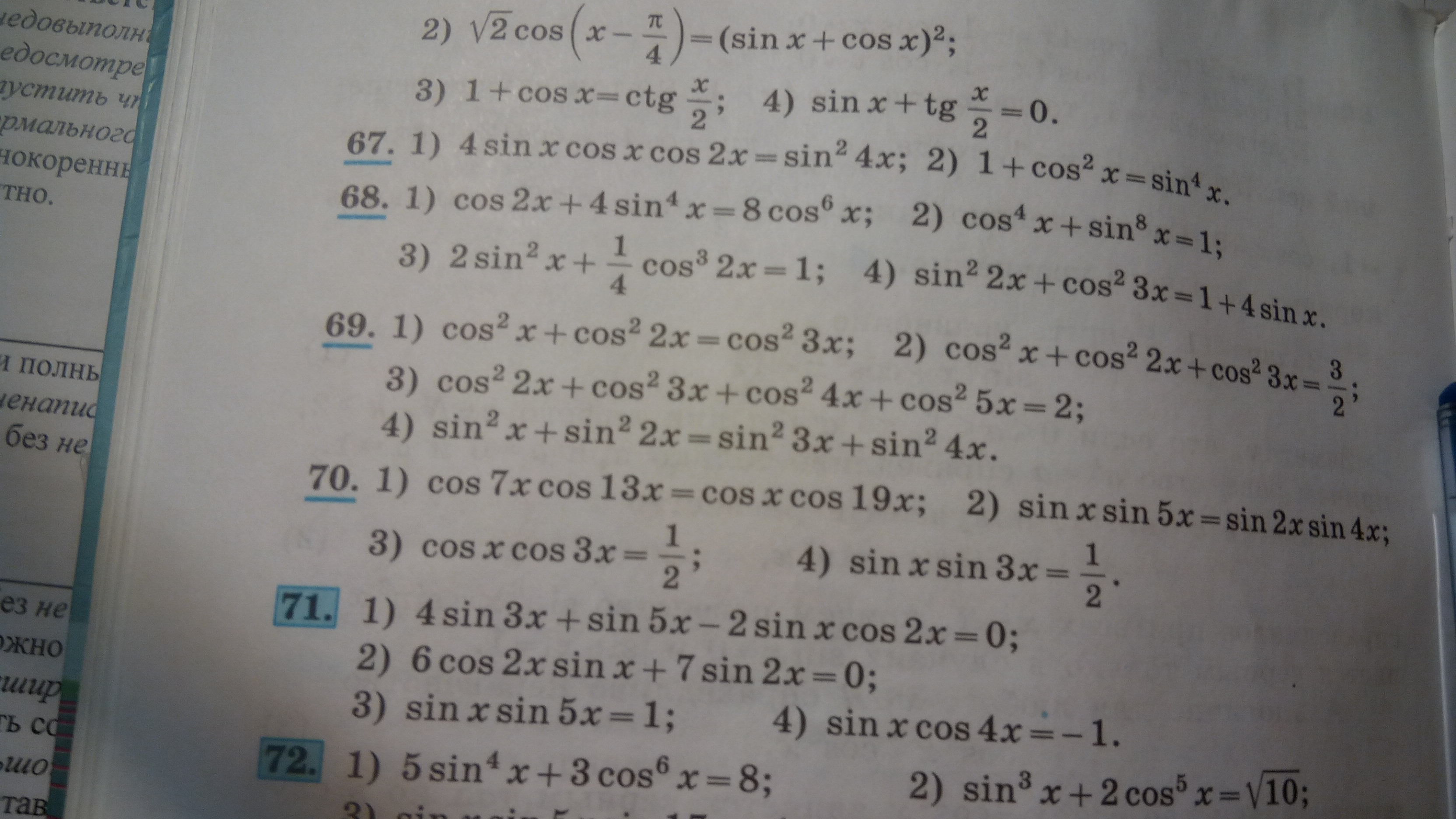
Ответы на вопрос
Ответил Аноним
0
Произведение равно нулю, если один из множителей равен нулю
Пусть
Обратная замена
Ответил Аноним
0
Спасибо) исправил)
Новые вопросы