Решить уравнение :
(схему Горнера не использовать)
Приложения:
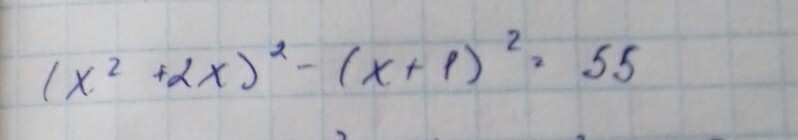
ТатМих:
Задание взято отсюда https://znanija.com/task/24933975
Не решать подобным образом,не доводить степень х до 4.
см решение с заменой
смотрю..исправьте опечатку
задание взято откуда*??)
отсюда. https://znanija.com/task/24927959
С нашего сайта,ссылка выше
отсюда. https://znanija.com/task/24927959 )))
Ответы на вопрос
Ответил Dимасuk
4
(x² + 2x)² - (x + 1)² = 55
(x² + 2x + 1 -1)² - (x + 1)² - 55 = 0
((x + 1)² - 1)² - (x + 1)² - 55 = 0
Пусть t = (x + 1)², t ≥ 0.
(t - 1)² - t - 55 = 0
t² - 2t + 1 - t - 55 = 0
t² - 3t - 54 = 0
По теореме, обратной теореме Виета, находим, что
t₁ + t₂ = 3
t₁·t₂ = -54
t₁ = 9
t₂ = -6 - не подходит
Обратная замена:
(x + 1)² = 9
(x + 1)² - 3² = 0
(x + 1 - 3)(x + 1 + 3) = 0
(x - 2)(x + 4) = 0
x = -4 или x = 2.
Ответ: x = -4; 2.
(x² + 2x + 1 -1)² - (x + 1)² - 55 = 0
((x + 1)² - 1)² - (x + 1)² - 55 = 0
Пусть t = (x + 1)², t ≥ 0.
(t - 1)² - t - 55 = 0
t² - 2t + 1 - t - 55 = 0
t² - 3t - 54 = 0
По теореме, обратной теореме Виета, находим, что
t₁ + t₂ = 3
t₁·t₂ = -54
t₁ = 9
t₂ = -6 - не подходит
Обратная замена:
(x + 1)² = 9
(x + 1)² - 3² = 0
(x + 1 - 3)(x + 1 + 3) = 0
(x - 2)(x + 4) = 0
x = -4 или x = 2.
Ответ: x = -4; 2.
t₂ = -3 - не подходит откуда минус 3 ?
t₂ =-6
да
Умничка )
Ответил mmb1
6
(x² + 2x)² - (x + 1)² = 55
(x² + 2x )² - (x²+2x+1) - 55 = 0
(x² + 2x )² - (x²+2x) - 56 = 0
замена m = (x²+2х)
m² - m - 56 = 0
D=1+4*56=225=15²
m₁₂=(1+-15)/2=-7 8
обратная замена
1. x²+2х=-7
x²+2х +7 = 0
D=4-28<0 нет решений в действительных числах
2. x²+2х=8
x²+2х - 8 = 0
D=4+32=36 = 6²
x₁₂=(-2+-6)/2=-4 2
Ответ -4 и 2
(x² + 2x )² - (x²+2x+1) - 55 = 0
(x² + 2x )² - (x²+2x) - 56 = 0
замена m = (x²+2х)
m² - m - 56 = 0
D=1+4*56=225=15²
m₁₂=(1+-15)/2=-7 8
обратная замена
1. x²+2х=-7
x²+2х +7 = 0
D=4-28<0 нет решений в действительных числах
2. x²+2х=8
x²+2х - 8 = 0
D=4+32=36 = 6²
x₁₂=(-2+-6)/2=-4 2
Ответ -4 и 2
Новые вопросы