Решить уравнение подробно
Приложения:
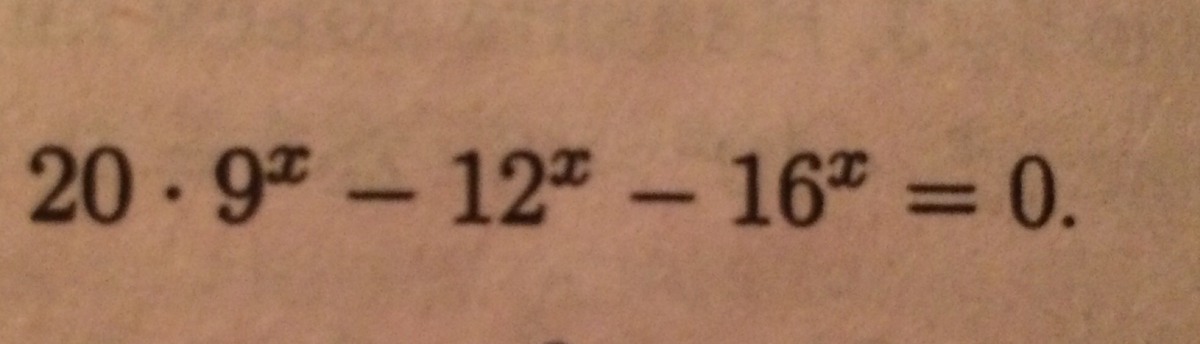
Ответы на вопрос
Ответил Аноним
0
Приложения:


Ответил kirichekov
0
20*9^x-12^x-16^x=0 |: 16^x
20*(9/16)^x-(12/16)^x-(16/16)^x=0
20*(3/4)^2x-(3/4)^x-1=0
(3/4)^x=t, t>0
20t²-t-1=0
D=81
t₁=1/4, t₂=-1/5, -1/5∉(0;∞)
t=1/4
(3/4)^x=1/4
log₃/₄(3/4)^x=log₃/₄(1/4)
x=log₃/₄(1/4)
если бы уравнение имело вид:
2*9^x-12^x-16^x=0,
то получилось бы:
2t²-t-1=0
D=9
t₁=1, t₂=-1/2. -1/2∉(0;∞)
t=1
(3/4)^x=1
(3/4)^x=(3/4)⁰
x=0
20*(9/16)^x-(12/16)^x-(16/16)^x=0
20*(3/4)^2x-(3/4)^x-1=0
(3/4)^x=t, t>0
20t²-t-1=0
D=81
t₁=1/4, t₂=-1/5, -1/5∉(0;∞)
t=1/4
(3/4)^x=1/4
log₃/₄(3/4)^x=log₃/₄(1/4)
x=log₃/₄(1/4)
если бы уравнение имело вид:
2*9^x-12^x-16^x=0,
то получилось бы:
2t²-t-1=0
D=9
t₁=1, t₂=-1/2. -1/2∉(0;∞)
t=1
(3/4)^x=1
(3/4)^x=(3/4)⁰
x=0
Новые вопросы
Математика,
1 год назад
Математика,
1 год назад