Решить уравнение 10/5-x + 3x-6/6-2x=3/(x-3)(x-1)
Ответы на вопрос
Ответил WhatYouNeed
0
Раскроем скобки:
Приведём подобные слагаемые:
Ответ:
Приложения:
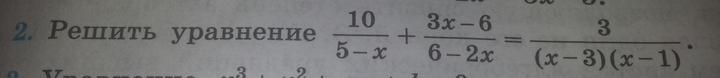
Новые вопросы