Решить систему матричным способом:
3x + 2y - z = 4
2x - y + 5z = 23
x + 7y - z = 5
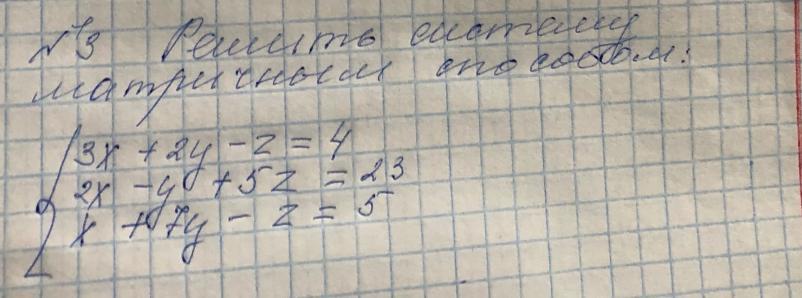
Ответы на вопрос
Ответ:
Пошаговое объяснение:
Система уравнений:
3x+2y-z=4
2x-y+5z=23
x+7y-z=5
( 3 2 -1 ) ( 4 )
A=( 2 -1 5 ) B=( 23 )
( 1 7 -1 ) ( 5 )
| 3 2 -1 |
Δ=| 2 -1 5 |=3·(-1)·(-1)+2·5·1+(-1)·2·7-(-1)·(-1)·1-2·2·(-1)-3·5·7=
| 1 7 -1 |
=3+10-14-1+4-105=-103
M₁₁=| -1 5 | =-1·(-1)-7·5=1-35=-34
| 7 -1 |
A₁₁=(-1)¹⁺¹·M₁₁=1·(-34)=-34
M₁₂=| 2 5 |=2·(-1)-1·5=-2-5=-7
| 1 -1 |
A₁₂=(-1)¹⁺²·M₁₂=-1·(-7)=7
M₁₃=| 2 -1 |=2·7-1·(-1)=14+1=15
| 1 7 |
A₁₃=(-1)¹⁺³·M₁₃=1·15=15
M₂₁=| 2 -1 |=2·(-1)-7·(-1)=-2+7=5
| 7 -1 |
A₂₁=(-1)²⁺¹·M₂₁=-1·5=-5
M₂₂=| 3 -1 |=3·(-1)-1·(-1)=-3+1=-2
| 1 -1 |
A₂₂=(-1)²⁺²·M₂₂=1·(-2)=-2
M₂₃=| 3 2 |=3·7-1·2=21-2=19
| 1 7 |
A₂₃=(-1)²⁺³·M₂₃=-1·19=-19
M₃₁=| 2 -1 |=2·5-(-1)·(-1)=10-1=9
| -1 5 |
A₃₁=(-1)³⁺¹·M₃₁=1·9=9
M₃₂=| 3 -1 |=3·5-2·(-1)=15+2=17
| 2 5 |
A₃₂=(-1)³⁺²·M₃₂=-1·17=-17
M₃₃=| 3 2 |=3·(-1)-2·2=-3-4=-7
| 2 -1 |
A₃₃=(-1)³⁺³·M₃₃=1·(-7)=-7
( A₁₁/Δ A₂₁/Δ A₃₁/Δ ) ( 34/103 5/103 -9/103 )
A⁻¹=( A₁₂/Δ A₂₂/Δ A₃₂/Δ )=( -7/103 2/103 17/103 )
( A₁₃/Δ A₂₃/Δ A₃₃/Δ ) ( -15/103 19/103 7/103 )
( 34/103 5/103 -9/103 ) ( 4 )
x=A⁻¹·B=( -7/103 2/103 17/103 ) · ( 23 )=
( -15/103 19/103 7/103 ) ( 5 )
( 34/103 ·4 +5/103 ·23 -9/103 ·5 ) ( 136/103 +115/103 -45/103 )
=( -7/103 ·4 +2/103 ·23 +17/103 ·5 )=( -28/103 +46/103 +85/103 )=
( -15/103 ·4 +19/103 ·23 +7/103 ·5) (-60/103 +437/103 +35/103)
( 206/103 ) ( 2 )
=( 103/103 )=( 1 )
( 412/103 ) ( 4 )
Ответ: x₁=2; x₂=1; x₃=4.