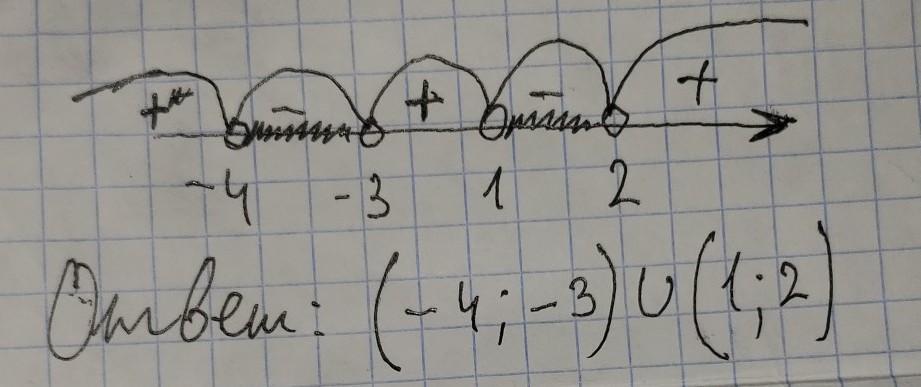Решить неравенство:
(x^2 + 2x)^2 - 11(x^2 + 2x) + 24 < 0
Пусть x^2+2x=t
Тогда t^2-11t+24<0
Дальше что? Как решать?
Ответы на вопрос
Ответ:
(-4 ; -3) и (1 ; 2)
Объяснение:
Верный ход решения:
Пусть x^2+2x=t
Тогда t^2-11t+24<0
Имеем:
t²-11t+24<0
Приравняем это выражение к 0 для нахождения минимального и максимального значения t
t²-11t+24=0
По теореме Виетта:
t1+t2=11
t1×t2=24
t1 = 3, t2 = 8.
Теперь у нас есть значения t. Представляем их в выражение x²+2x=t
1) При t= 3
x²+2x=3
x²+2x-3=0
По теореме Виетта:
x1+x2= -2
x1×x2= -3
x1= -3 ; x2=1
2) При t=8
x²+2x=8
x²+2x-8=0
По теореме Виетта:
x1+x2= -2
x1×x2= -8
x1= -4 ; x2= 2.
Получаем 4 корня x: -4 , 2 , -3 , 1
Возвращаемся к главному неравенству и находим при каких X оно будет меньше нуля:
Для этого рисуем прямую и отмечаем корни в порядке возрастания, рисуем между корнями дуги и отмечаем их знак, начиная с самой правой дуги (она положительная, т.к. все x в неравенстве положительные) и закрашиваем те дуги, в которых стоит знак минус ( - ). Записываем ответ в виде интервалов:
(-4 ; -3) и (1 ; 2)